Classical Kinetic Theory of Gases: A Crash Review
The classical kinetic theory of gases is usually covered in a basic
chemistry class. The key assumption is:
In the absence of significant molecular interactions,
- The average kinetic energy of a molecule is independent of the
kind of molecule.
- The average kinetic energy of a molecule is directly
proportional to the absolute temperature.
This is not intended to be a rigorous presentation.
Notes:
- For a gas, "standard conditions" (when a substance is a gas
under such conditions) is defined as a temperature of 0°C and a
pressure of 1 atm(osphere). This is a historical artifact.
- The volume of a mole of ideal gas molecules at "standard
conditions" is approximately 22.4 liters.
Classical Kinetic Theory Survival 101
What is the "average kinetic energy"?
What are "significant molecular interactions"?
What is the probability distribution for the speed of the molecules?
What is the "perfect gas law" i.e. "ideal gas law"?
What about Boyle's, Avogadro's, and Charles' laws?
When do evaporation and condensation become impossible?
Ideal gas law from average kinetic energy
Noble gases i.e. monoatomic gases: Classical Kinetic Theory Survival 201
Heat capacity of an ideal noble gas at constant volume
Heat capacity of a noble gas at constant pressure
When volume and molecular interactions matter: Van der Waals Equation
Van der Waals' Equation
Estimating Van der Waals constants from critical temperature and pressure
The Van der Waals equation as a Laurent series in V, i.e. power series in 1/V: the Boyle temperature
Interesting resources
Gas law calculator [JavaScript]
Obscure real gas laws -- CCL
Obscure real gas laws
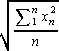 We use the root-mean-square average [RMS average] to compute the
average (RMS) kinetic energy. Cf. the expression on the right. For
hydrogen [H2] gas at 0°C, the average speed of a
hydrogen molecule is about 1.84·10³
meters/second [m/s]. Part of the derivation of the
Maxwell-Boltzmann probability distribution for the speed of the
molecules defines absolute temperature so that this is the
expression for the average kinetic energy of a molecule of gas:
T is absolute temperature, and k is Boltzmann's constant. I would
assume that this expression fails when the temperature is low
enough to cause the Maxwell-Boltzmann probability distribution to
require quantum corrections...but I don't know this.
We use the root-mean-square average [RMS average] to compute the
average (RMS) kinetic energy. Cf. the expression on the right. For
hydrogen [H2] gas at 0°C, the average speed of a
hydrogen molecule is about 1.84·10³
meters/second [m/s]. Part of the derivation of the
Maxwell-Boltzmann probability distribution for the speed of the
molecules defines absolute temperature so that this is the
expression for the average kinetic energy of a molecule of gas:
T is absolute temperature, and k is Boltzmann's constant. I would
assume that this expression fails when the temperature is low
enough to cause the Maxwell-Boltzmann probability distribution to
require quantum corrections...but I don't know this.
Anything that would measurably alter the quantity of the gas. A non-exhaustive list would include:
- The absolute temperature is high enough to ionize some of the molecules. [That is a plasma, not a gas!].
- Phase changes: sublimation (to or from a solid), evaporation (from liquid), or condensation (to liquid). Evaporation and
condensation don't work above the critical temperature.
- Chemical reactions. Even if the chemical species reach equilibrium, the reaction will respond to changes in the physical
parameters (temperature, pressure, and volume), thus altering the composition of the gas. Even if the reaction doesn't alter the
molecule count, it may well affect the temperature.
There are at least two interactions that do not affect the basic assumptions of classical kinetic gas theory, but do
affect more detailed equations.
- Molecules don't overlap.
- Molecules that are far part tend to polarize each other, and then attract each other (very weakly).
Historically, formally deriving this algebraically is a test of Quantum Mechanics. There are at least two possible approaches to
this; both are not that clean. It was empirically extrapolated by James Clerk Maxwell (1831-1879) in 1860, about five to six decades
before Quantum Mechanics was beginning to be formulated.
At sufficiently intermediate temperatures (well above the boiling point of liquid helium, but below thermal ionization of the
gas), the following differential equation is a good approximation (i.e., not the accuracy-limiting factor):
dN = N·4π(m/[2πkT])3/2e-mv²/[2kT] v²dv
Integrate the right-hand side on v from the lower bound of the
classical velocity to the upper bound of the classical velocity in
question, to get the expected number of molecules with a speed in that range. In the above:
- m: mass of the molecule
- v: classical velocity
- N: number of molecules
- k: Boltzmann's constant. Value depends on the units of measurement for velocity and absolute temperature.
- T: absolute temperature.
We call this the Maxwell-Boltzmann probability distribution for the speed of a molecule. The above formulation of the equation has the
advantage of highlighting the ratio m/(kT)...which is the only occurence of k, m, and T. If we set a :=
m/(kT), we can simplify the above differential equation to
dN = N·[2/π]1/2(α)3/2e-αv²/2 v²dv
Unless we are concerned about very small Lorentz corrections, it is not worth the effort to find the General-Relativistic version of
the above equation -- in practice, the gas will ionize from high temperatures before the corrections become significant.
Gravity-field emulation techniques (if necessary) should suffice.
However, the algebraic morass from which the formula comes does have significant corrections to a key part at low
temperatures. The corrections depend on the distinction between bosons and fermions...and seriously affect the form of the
equation.
The perfect gas law equation is:
PV = nRT
In the above,
- P: pressure
- V: volume
- n: moles of gas molecules
- R: molar gas constant. The value depends on the units of
measurement for pressure, volume, and absolute temperature.
- T: absolute temperature.
Historically, a formal test of the Maxwell-Boltzmann speed
distribution law is the derivation of the perfect gas law from it.
This is another algebraic morass. This derivation ignores both
volume exclusion and the normally-weak electromagnetic attraction
between molecules. The induced deviations are most extreme when a
gas is close to changing phase.
- The finite volume of the molecules tends to increase the volume
above an ideal gas' volume.
- Molecules tend to attract each other slightly when far away
(this is a weak electromagnetic effect). This tends to make the
pressure less than an ideal gas' pressure.
Errors tend to be minimal far away from both the boiling point and
critical pressure of a gas. For gases similar to the Earth's
atmosphere, the errors are generally less than 1% for room
temperature or higher, and pressures below 10 atm.
NOTE: The derivation of the ideal gas law does
assume that gravity is insignificant: that is, it is legitimate to
represent the center-of-mass trajectories of the gas molecules
between collisions as straight lines. Two obvious violations of
this are strong gravity fields (neutron star or stronger), and
protostars. In both cases, the ideal gas law works on scales small
enough to not see the curvature in the center-of-mass
trajectories.
These are all partial versions of the perfect gas law. Using
variable names as defined above:
- 1662: (Robert) Boyle's (1627-1691) law:
PV = constant when T, quantity of gas constant.
- 1787: (Jacques Alexander) Charles (1746-1823) reported that
different gases expanded by the same fraction for the same rise in
temperature.
- 1801: Dalton conjectures the law of partial pressures:
molecular type does not matter when figuring the overall pressure
of a gas...so the partial pressure for a given gas compound is the
percentage (by molecule count) of that compound in the gas. Add the
partial pressures to get the total pressure.
- 1802: (Joseph Louis) Gay-Lussac (1778-1850) empirically
determines an absolute temperature scale. He refines Charles' law to:
V/T = constant when pressure, gas quantity constant.
T must be an absolute temperature. He found that the Celsius scale
could be converted to an absolute temperature scale [now called
Kelvin] by adding about 273 degrees to the Celsius scale.
- 1805: Gay-Lussac started experimenting with gases that
chemically reacted. He finds that they reacted in ratios defined by
small integers. For instance, 2000 ml of hydrogen + 1000 ml of
oxygen completely reacted to form water. Also, 1000 ml of carbon
monoxide reacted with 500 ml of oxygen to form 1000 ml of carbon
dioxide.
Obviously, some of these chemical names are translated into our
nomeclature. As a conceptual tool, reaction equations (and chemical
formulae as we know them) don't exist yet. In particular, at
this stage what is known about carbon monoxide and carbon dioxide
is that they are both gases, and they both contain only carbon and
oxygen.
- 1811: Amadeo Avogadro (1776-1856) proposes a hypothesis
(Avogadro's law): equal volumes of dilute gases contain equal
numbers of molecules. Avogadro's law's practical applications
escape notice.
- 1858: Stanislao Cannizarro (1826-1910) showed how to apply
Avogadro's law systematically. This immediately solves the
questions of both correct atomic weight ratios and correct
formulae.
For instance, before 1858 it was unclear whether the correct
chemical formula for water was H2O or HO. In our
nomeclature, water is H2O...and HO is a hydroxide
radical without its electron, imminently about to resume its normal
formula HO-.
- At this point, the perfect gas law
PV = nRT
can instantly be obtained (aside from how to measure the quantity
of the gas n) as an algebraic extrapolation of Boyle's, Charles',
and Avogadro's laws.
- 1860: James Clerk Maxwell (1831-1879) empirically extrapolates
the Maxwell-Boltzmann probability distribution. The algebraic
derivation of the perfect gas law, from the Maxwell-Boltzmann
probability distribution, is a formal test of the
Maxwell-Boltzmann probability distribution. Starting in
1858, the perfect gas law is capable of falsifying probability
distributions for the speed of molecules.
- 1920: Otto Stern attempts an empirical verification of the
Maxwell-Boltzmann probability distribution. By heating a tungsten
wire, he constructed a beam of silver atoms emitted at about
1200°C By using a system of slits and a rotating drum, it was
possible to measure how many emitted silver atoms were travelling
in various speed ranges. By 1947, empirical verifications can
measure agreement with the Maxwell-Boltzmann probability
distribution to within 1% or so.
Thomas Andrews [1813-1885] discovered that for a pure gas, the
distinction between the liquid and gas phases vanishes at the
"critical temperature". This is formally called the "continuity of
the gas and liquid phases". Qualitatively, there is still a
difference (gases are obviously compressible, liquids aren't very
compressible).
- Above the critical temperature: the gas can be compressed into
a liquid without a phase change.
- Below the critical temperature: increasing the pressure
eventually causes the gas to saturate, followed by condensation
into a liquid.
Consider a single gas molecule with mass m, and assume that its collisions with a wall are both practically instantaneous, and perfectly elastic. To further simplify things, let's
consider a cubical container of volume V, whose sides are aligned with the x-y-z cartesian coordinate system. [The sides being of length ³√V.]
The molecule has velocity v := (vx,vy,vz). As the collisions are perfectly elastic, each collision with a wall
only changes the sign of the corresponding coordinate in the velocity. The magnitude of the impulse at a collision with a y-z plane wall is then 2m|vx|.
For an ideal gas, the distance in the x-coordinate traveled between two collisions with the same y-z wall is
We thus get an average magnitude of orthogonal force on each y-z wall of
i.e.
After conducting similar calculations for vy and the x-z walls, and vz and the x-y walls, we add the magnitudes of force on all six walls:
| 2m|vx|²+2m|vy|²+2m|vz|² |
| ³√V |
But this reduces (by definition of Euclidean norm of a vector) to an expression in the kinetic energy of the gas molecule.
When we have enough particles to average, we can replace m|v|²/2 with the average kinetic energy. In particular, for one mole of ideal gas
we have the following as the magnitude of force on all six walls:
Since each wall has an area of (³√V)², and the molecules of an ideal gas have zero length, the pressure on a single
wall of this cube from a mole of ideal gas is
And thus we get PV=RT for one mole of ideal gas. With n as the number of moles, this recovers the ideal gas law PV=nRT.
This depends on the definition used in the Maxwell-Boltzmann
probability distribution for the speed of the molecules of the
(noble) gas. The average RMS kinetic energy of
per molecule immediately translates to a total kinetic energy of
per mole, where k, T, and R are defined as before. Informally, we
computed the average RMS kinetic energy per molecule from
the total kinetic energy per mole, so "obviously" we can reverse
the procedure. We might suspect that R/k is the conversion factor
from "per molecule" to "per mole"...in which case it should be
Avogadro's constant. Skimming the fundamental constants list at the
 U.S.
NIST, we find that this is indeed the case empirically.
U.S.
NIST, we find that this is indeed the case empirically.
We differentiate by T to find the heat capacity in
deg-1mol-1:
(d/dT)([3/2]RT) deg-1mol-1 =
[3/2]R deg-1mol-1
Thus, the heat capacity CV of an ideal noble gas is
(3/2)R deg-1mol-1. Numerically (NIST data):
1.5.[8.314 472 ± 0.000 015]
J.mol-1K-1, which is approximately
12.471708 ± 0.000 023]
J.mol-1K-1.
Real noble gases approximate this very well. This does not apply
to more complicated gases, because they have additional methods of
storing heat besides kinetic energy.
This depends on the perfect gas equation (and has all of that
equation's foibles). The general technique is to notice that when
the volume of a gas increases at constant pressure [say, in an
effectively friction-free gas-tight piston], the work done by an
increase in volume dV is P dV. If we want to increase the volume of
a gas in such conditions by increasing the temperature, the
relevant quantity is dV/dT. We can implicitly differentiate the gas
law by T, holding n, R, and P constant:
(d/dT)(PV) = (d/dT)(nRT)
i.e.
P(dV/dT) = nR
i.e. P dV = nR dT . This heat energy is in addition to that
required to heat the gas at constant volume, so the heat capacity
CP at constant pressure is
R deg-1mol-1 greater than the heat capacity
CV at constant volume. That is, CP for an
ideal noble gas is (5/2)R deg-1mol-1.
Numerically (NIST data): 2.5.[8.314 472 ± 0.000
015] J.mol-1K-1, which is
approximately 20.786180 ± 0.000 038]
J.mol-1K-1.
Real noble gases approximate this very well. Again, this does
not apply to more complicated gases -- for the same reason.
The above content was adapted from Linus Pauling's "General
Chemistry", ©1970 [Dover 1988 reprint].
Purdue on Van der Waal's equation
In 1873, the Dutch physicist Johannes van der Waals extrapolated
how to implement first-order corrections to the ideal gas law, that
accounted for molecular volume and the small attractive forces
responsible for the gas-liquid phase distinction at low
temperatures. These extrapolations require empirical constants:
[P+(an²/V)][V-nb]=nRT
In addition to the prior notation, we now have two empirical Van
der Waals constants:
- a: a proportionality constant measuring the weak
electromagnetic attractive forces between the gas molecules.
- b: molar volume of the gas molecules.
When going from a sufficiently chemically pure gas, to a realistic
mixture: b (molar volume) isn't too difficult -- but a poses some
interesting questions.
Phase change diagrams for a Van der Waals gas
NOTE: this page uses different notation : their N is my n,
and their k is my R. (Confusing! I need the Boltzmann constant...).
For a sufficiently chemically pure gas: Let Tc be the
critical temperature, Pc be the critical pressure, and
Vc be the critical volume.
["Critical temperature" is what we've seen before. "Critical
pressure" is the limit of the vapor pressure of the liquid as the
liquid's temperature approaches the critical temperature from
below. "Critical volume" is (similarly) the limit of the volume of
the liquid as the liquid's temperature approaches the critical
temperature from below. Another way of thinking about it is as the
liquid is brought to its critical temperature from below,
eventually the vapor (immediately after vaporization) will approach
the liquid in density. The critical state then can be thought of as
occuring when the vapor density equals the liquid density.]
Then, for a perfect Van der Waals gas, both Linus Pauling and
the above link report that:
| Tc = 8a/(27bR) |
Pc = a/(27b²) |
Vc = 3bn |
Linus Pauling reports that, in practice, the critical temperature
and critical pressure are much closer to the theoretical values
than the critical volume, and that the pragmatic approximation to
critical volume is usually close to 2.25bn. That means it is
possible to estimate a and b from the critical temperature and
critical pressure (a minor algebra exercise).
EXERCISE: The natural temperature, pressure and volume units for
a Van der Waals gas are the critical temperature, critical
pressure, and critical volume. That is: for a mole of gas [n=1],
when the units are changed to T' := T/Tc, P' :=
P/Pc, and V' := V/Vc, the Van der Waals
equation algebraically reduces to:
[P'+3/V'²][3V'-1] = 8T'
The ' marks are to indicate changed coordinates, not first
derivatives.
EXERCISE: In SI units, a is m³·K/mol. b is m³/mol, i.e. molar volume.
Most chemically pure gases have the same physical properties at
the critical state when the units are normalized this way. This is
called the Law of Corresponding States. It also suggests that any
proposed improvements on the Van der Waals equation also have this
property.
Phase change calculator
The Van der Waals gas equation can be rewritten as the leading
coefficients of a Laurent series in V, when the number of moles n
is set to 1:
PV/(RT) = 1 + [b-a/(RT)]/V + b²/V² + ...
We define a Boyle temperature TBoyle as a temperature at
which the "linear" term of the Laurent series is 0.
TBoyle is not useful for an ideal gas [no correction
terms]. For a Van der Waals gas, an algebraic exercise indicates
that TBoyle = a/(bR).
Opinions, comments, criticism, etc.? Let me know about it.
Return to the Math page, or the main page.
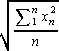 We use the root-mean-square average [RMS average] to compute the
average (RMS) kinetic energy. Cf. the expression on the right. For
hydrogen [H2] gas at 0°C, the average speed of a
hydrogen molecule is about 1.84·10³
meters/second [m/s]. Part of the derivation of the
Maxwell-Boltzmann probability distribution for the speed of the
molecules defines absolute temperature so that this is the
expression for the average kinetic energy of a molecule of gas:
We use the root-mean-square average [RMS average] to compute the
average (RMS) kinetic energy. Cf. the expression on the right. For
hydrogen [H2] gas at 0°C, the average speed of a
hydrogen molecule is about 1.84·10³
meters/second [m/s]. Part of the derivation of the
Maxwell-Boltzmann probability distribution for the speed of the
molecules defines absolute temperature so that this is the
expression for the average kinetic energy of a molecule of gas: