Trigonometry: A Crash Review
(my science fantasy
novel)
|
|
|
|
|
|
|
|
|
|
|
|
|
Unfortunately, for much of this subject, there is no substitute for
brute memorization. This course is often used as pre-calculus.
"Algebra masters" will have a much smaller memorization load than
other students. [I mean College Algebra, not the higher-math
version.] Much of this subject is highly dependent on either
calculators+ or tables [slide rules have been passé since the
electronic calculator, but could be used.] Traditionally, this
subject relies on some familiarity with "College Algebra", but not
an intensive mastery.
Easily review trigonometry as you work at a computer!
Note: in many places, I will mention algebraic identities. For
serious students who are either algebra-deficient or have to use
the material under time pressure, I highly recommend working
through "all of the plausible forms" and memorizing them. This
usually means algebraic isolation of various variables in the
equations, and figuring out how to use multiple equations in one
problem. Currently, I am not providing the homework that is
required to learn the material. I would like to partially remedy
this deficiency. [No timetables!]
Note: There are several kludge notations lurking in this crash
review:
- SQRT for "square root" (correctly notated for 2, 3, 5, and
6)
- pi for π (correctly notated outside of
popup text for pictures)
I will remove instances of these kludge notations, without advance
warning, when it is convenient in my schedule to do so.
Trigonometry Survival 101 -- basic material [not coordinate
geometry]
What are these trigonometric [trig] functions, anyway?
What does a negative angle (measure) mean?
Why should I know the generic right triangle?
What are the reference triangles?
Why should I know the unit circle?
How does "wrapping the real number line" around the unit circle work?
What are the triangle area formulae?
What is the law of sines?
What is the law of cosines?
What are the angle sum, difference, and/or doubling formulae?
What are the angle halving formulae?
What are the trig(onometric) sum and difference formulae?
What are the trig(onometric) product formulae?
Trigonometry Survival 201 -- useful material, but not in your standard Trigonometry course
Reference values -- 15° and 75°
i.e. π/12 and 5π/12
radians i.e. 100/6 and 500/6 gradients
Reference values -- 18°,
36°, 54°, and 72° i.e. π/10,
π/5, 3π/10, and
2π/5 radians i.e. 20, 40, 60, and 80
gradients
Instant numerical trigonometric tables
for sin, cos, and tan near 0
Formula Lists
Angle classifications
Angle relations
Arc length from central angle and radius
Cofunction relations
Supplementary angle relations
Algebraically even and odd trigonometric functions
Basic reference tables
Trigonometric function evaluation from sides of a right triangle
Trigonometric function signs from quadrants of the unit circle
Trigonometric functions that are multiplicative inverses of each other
Trigonometric functions in terms of sin(X) and cos(X)
Pythagorean Theorem
Pythagorean Identities
Self-quizzes
All of these require JavaScript.
Reference values: sin, cos of 0°, 30°, 45°, 60°, 90°
Reference values: sin, cos of 0°, 15°, 30°, 45°, 60°, 75°, 90°
Reference values: sin, cos of 0°, 18°, 36°, 54°, 72°, 90°
A Vastly Incomplete Selection of Web Resources
Trig FAQ, J. David Eisenberg
Short Course in Trigonometry, David E. Joyce
Introduction to Trigonometry, Johan. Claeys [and a possible mirror]
Physics
Dept., University of Guelph
Trigonometry
Overview, Kenny Felder
Calculus
2000, Mr. Marco. Go to the bottom of the page, then
start scrolling back upwards. There's trigonometry down there.
Basic Trigonometry, Purdue
Web Graphing
Calculator
Web evaluator for sin, cos, tan, and arctan
Measures,
Shape, and Space: Also has some links about coordinate systems and
Euclidean geometry.
What are these trigonometric [trig]
functions anyway?
Their names are:
- sine [sin]
![The hatch marks for sin(x)=1 are at pi/2 and -3pi/2. The hatch marks for sin(x)=-1 are at -pi/2 and 3pi/2. Sin(x)=0 [intersects the x-axis] at ±2pi, ±pi, and 0](grafx/RefSin.gif)
- cosine [cos]

- tangent [tan]
- cotangent [cot]
- secant [sec]
- cosecant [csc]
These functions have a single argument, and take angles. By the
heuristic of "wrapping the real number line around the unit
circle," we can think of these functions as taking real numbers as
arguments. Note that in "stratosphere" math, the above approach is
very painful; other techniques are used to define these functions.
These techniques are the ones which calculators are programmed with
-- but they're not appropriate for this section.
Incidentally, there are three angle units listed on my HP-48SX:
degrees, radians, and gradients. [Gradients are not commonly used
in the U.S.A.] To rebuild the conversion formulae, remember:
1 circle = 360 degrees = 2π radians = 400 gradients.
- We inherited degrees from Babylonia. There are 60 minutes in a
degree, and 60 seconds in a minute. [When dealing with the Earth's
rotation in astronomy, the Earth rotates "about" 1 angular degree
in 4 solar-day minutes. The Earth rotates 1 degree in 4
sidereal-day minutes.] Also, a nautical mile is "about" 1
arc-minute on the Earth's surface. This would be exact if the Earth
was a perfect sphere. A common notation for, say, 3 degrees 4
minutes 5 seconds is 3°4'5".
- Radians are the "natural" angle unit when dealing with
"stratosphere" math. The defining formulae for sin and cos are much
simpler then. Radians also behave better if you have to deal with
calculus [deriviatives and integrals].
- I don't know much about the history of gradients.
A right angle is 1/4th of a circle;
i.e. 90°, π/2 radians, or 100
gradients. I will use the common symbol  for a right angle, in the rest of this crash
review. An angle larger than 0, but smaller than a
for a right angle, in the rest of this crash
review. An angle larger than 0, but smaller than a  , is called an acute
angle. An angle larger than a
, is called an acute
angle. An angle larger than a  , but smaller than half a
circle, is called an obtuse angle.
, but smaller than half a
circle, is called an obtuse angle.
 is a standard symbol in the literature (although
found more often in geometry texts than trigonometry texts). When
it shows up in a diagram, it designates the labeled angle as a
right angle.
is a standard symbol in the literature (although
found more often in geometry texts than trigonometry texts). When
it shows up in a diagram, it designates the labeled angle as a
right angle.
For the record: Triangles are constructed by picking three
points, then joining each pair by a straight line segment. We
assume we can neglect curvature of the surface. That is, we assume
the geometry is Euclidean. [You will not get the same kind of
triangles on a sphere as on a flat desk or piece of paper. The
sphere is visibly curved, the desk and the flat piece of paper are
not supposed to be curved.] I will occasionally use the fact the
geometry is Euclidean.
The sum of the three (interior) angles of a triangle is half a
circle, i.e. 180° or π radians or 200
gradients. I will sometimes denote this by 2 in the rest of this crash review; this is
not standard notation. An implicit exercise will be
translating 2
in the rest of this crash review; this is
not standard notation. An implicit exercise will be
translating 2 to angular measure [degrees, radians,
and/or gradients.].
to angular measure [degrees, radians,
and/or gradients.].
If we pick a point on a straight line, the two parts of the
straight line formed by taking out the point form an angle of half
a circle, i.e. 180° i.e. π radians
i.e. 200 gradients. In general, I will omit "interior" when talking
about angles of a triangle.
We say a triangle, that contains a right angle, is a right
triangle. If a triangle has two sides of equal length and one side
of different length, we call it an isosceles triangle. If a
triangle has three equal sides, we say it is an equilateral
triangle.
Note:
- For an isosceles triangle, the two angles opposite the sides
with equal length (i.e., the two angles whose bounding sides have
one of the two sides of equal length, and the side with different
length) are equal.
- For an equilateral triangle, all three angles are equal, and
equal 60° i.e. π/3 radians i.e. 200/3
gradients.
The angle measure in radians is simply arc length on a circle of
radius 1. In general, for a circle with radius R and an arc with
central angle X in radians,
There are two pictures to keep in mind here:
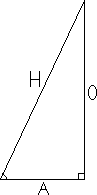 the generic right triangle, and
the generic right triangle, and 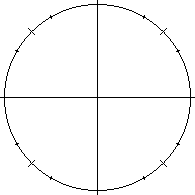 the unit circle.
the unit circle.
Here, A, H, and O are acronyms for Adjacent [to angle],
Hypotenuse, and Opposite [from angle], respectively.
What does a negative angle (measure) mean?
First of all, all physical angles have some size. We cannot
visualize an angle with negative physical size. They do not exist
in anything sufficiently similar to the physical space we live
in.
However, (especially when dealing with the unit circle), it is
often convenient to measure angles in a specific direction:
counterclockwise. [I'm not going to digress into "stratosphere"
math now, but that is dictating the convention here.]
Then, a negative sign means we are measuring the angle
"unconventionally", i.e. clockwise.
This will simplify the use of some of the trigonometric
identities we are going to look at.
Why should I know the generic right triangle?
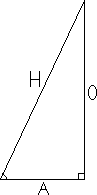 Given a
right triangle, the trig function values for the two acute angles
[angles smaller than a right angle] can be computed without knowing
the angles. I prefer to remember the formulae this way [X is an
angle]:
Given a
right triangle, the trig function values for the two acute angles
[angles smaller than a right angle] can be computed without knowing
the angles. I prefer to remember the formulae this way [X is an
angle]:
- sin(X) = O/H; csc(X) = H/O
- cos(X) = A/H; sec(X) = H/A
- tan(X) = O/A; cot(X) = A/O
In all cases, division by zero should be interpreted as
"undefined".
If H=1, then O and A are simply cos(X) and sin(X).
A mnemonic for the formulae for sin(X), cos(X), and tan(X) is
the (fictitious) Indian Chief Soh-cah-toa, who had no problems with
this part of trigonometry. [I got this from Mr. Coole, a long time
ago -- I was in grade school then.]
The way I wrote the formulae, above, emphasizes the following
identities:
- sin(X)csc(X)=1
- cos(X)sec(X)=1
- tan(X)cot(X)=1
These identities do work when both functions involved are defined
for the angle X, regardless of size.
Another fact, of some use, is the Pythagorean theorem:
H²=A²+O². If we relabel A as a, O as b, and H as c,
we get the familiar form of the Pythagorean theorem:
c²=a²+b². This only works for right
triangles. The
generalization of the Pythagorean theorem to non-right triangles is
called the law of cosines.
A common strategy is to memorize how to compute tan(X), cot(X),
sec(X), and csc(X) in terms of sin(X) and cos(X), and then reduce
everything to this. This is not necessarily the least painful way
to do a trig problem, but it is often more important to start the
problem, than figure out how to do it elegantly. [EXERCISE: derive
this from the A, H, O formulation for acute angles. The formulae
work for arbitrary angles.]
- tan(X)=sin(X)/cos(X)
- cot(X)=cos(X)/sin(X)
- sec(X)=1/cos(X)
- csc(X)=1/sin(X)
The generic right triangle also motivates some terminology [which
we inherited from twelfth century Arabian mathematics].
First of all, we say two angles are complementary if they add up to a right
angle. That is, for an angle X, we say  -X is complementary to X.
-X is complementary to X.
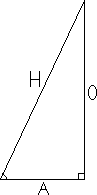 For instance, the angle in the upper right-hand corner is
complementary to, i.e. the complement of, the marked angle in the
lower left-hand corner.
For instance, the angle in the upper right-hand corner is
complementary to, i.e. the complement of, the marked angle in the
lower left-hand corner.
A related piece of terminology is supplementary angles: two angles are
said to be supplementary if they add up to half a circle, i.e.
180° i.e. π radians i.e. 200
gradients. That is, 2  - X is supplementary to
the angle X. To get an intuition for this, draw a unit circle with
the horizontal axis.. Draw an arbitrary radius from the center to
somewhere on the unit circle. The two angles formed between the
radius, and the horizontal axis, are supplementary.
- X is supplementary to
the angle X. To get an intuition for this, draw a unit circle with
the horizontal axis.. Draw an arbitrary radius from the center to
somewhere on the unit circle. The two angles formed between the
radius, and the horizontal axis, are supplementary.
Now, let's look at the trig function-computation rules again:
- sin(X) = O/H; csc(X) = H/O
- cos(X) = A/H; sec(X) = H/A
- tan(X) = O/A; cot(X) = A/O
What happens if we swap A and O in these formulae? This is
computing the trig function of the complement of X, i.e.  -X. Go ahead, do it :) It's easy.
-X. Go ahead, do it :) It's easy.
What you should get are the cofunction identities:
- sin(
 -X)=cos(X)
-X)=cos(X)
- cos(
 -X)=sin(X)
-X)=sin(X)
- tan(
 -X)=cot(X)
-X)=cot(X)
- cot(
 -X)=tan(X)
-X)=tan(X)
- sec(
 -X)=csc(X)
-X)=csc(X)
- csc(
 -X)=sec(X)
-X)=sec(X)
We say that sin and cos [sine and cosine], tan and cot [tangent and
cotangent], and sec and csc [secant and cosecant] are cofunctions,
and that the trig function of the complement of an angle X is equal
to the trig cofunction of the angle. This is explicitly in the
function names: cosine is the cofunction of sine, cotangent is the
cofunction of tangent, and cosecant is the cofunction of secant.
These identities do work for arbitrary angles. If one side is
undefined, both sides are undefined.
What are the reference triangles?
The reference triangles are right triangles that are "easy to
construct". They provide easily-memorized values for the angles
with measure 30°, 45°, and 60°, i.e. π/6,
π/4, and π/3 radians, i.e. 100/3,
50, and 200/3 gradients.
There are two reference triangles. They [in the U.S.A.] are
known by their degree names:
- 45-45-90 [constructed from square]
- 30-60-90 [constructed from equilateral triangle]
The 45-45-90 (degree) right triangle can be constructed from a
square with sides of length one. The hypotenuse is the line
connecting two opposite vertices of the square; it has length  by
the Pythagorean Theorem. [Exercise:
compute this!] The legs of the triangle are sides of the square.
Note: 45° is its own complementary angle.
by
the Pythagorean Theorem. [Exercise:
compute this!] The legs of the triangle are sides of the square.
Note: 45° is its own complementary angle.
 When we put A=1=O and H=
When we put A=1=O and H= into the generic right triangle, we get:
into the generic right triangle, we get:
- sin(45°) =
 /2
/2
- cos(45°) =
 /2
/2
- tan(45°) = 1
- cot(45°) = 1
- sec(45°) =

- csc(45°) =

[Do it.]
The 30-60-90 triangle is constructed from an equilateral
triangle with sides of length 2. We put one side on the horizontal
axis, and bisect the angle opposite this side. [Note that an
equilateral triangle has three vertex angles, all of which are
60°.]
 We now have a hypotenuse of length 2, one leg of length 1 [from
bisecting the horizontal side], and one side with length
We now have a hypotenuse of length 2, one leg of length 1 [from
bisecting the horizontal side], and one side with length  [from the bisecting line].
[from the bisecting line].
We get:
- sin(30°)=cos(60°)=½
- cos(30°)=sin(60°)=
 /2
/2
- tan(30°)=cot(60°)=1/
 =
= /3
/3
- cot(30°)=tan(60°)=

- sec(30°)=csc(60°)=2/
 =(2
=(2 )/3
)/3
- csc(30°)=sec(60°)=2
[Again, do it.]
Why should I know the unit circle?
The unit circle provides a picture on which to memorize reference values of the trig functions.
 Think of it as the set of
possible endpoints for a length 1 hypotenuse H, with one endpoint
of H fixed at the origin. We can construct generic right triangles
with hypotenuse 1 in it. Pick a point on the circumference, draw a
line segment from it to the origin, and then draw a perpendicular
line segment down to the x-axis.
Think of it as the set of
possible endpoints for a length 1 hypotenuse H, with one endpoint
of H fixed at the origin. We can construct generic right triangles
with hypotenuse 1 in it. Pick a point on the circumference, draw a
line segment from it to the origin, and then draw a perpendicular
line segment down to the x-axis.
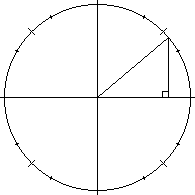 Notice that
the coordinates of the vertex, in Cartesian coordinates, is
(cos(X), sin(X)), where X is the central angle. The horizontal side
(on the x-axis) is A, and the vertical side (parallel to the
y-axis) is O. The radius (length 1) is H. The slope of the
hypotenuse H is tan(X).
Notice that
the coordinates of the vertex, in Cartesian coordinates, is
(cos(X), sin(X)), where X is the central angle. The horizontal side
(on the x-axis) is A, and the vertical side (parallel to the
y-axis) is O. The radius (length 1) is H. The slope of the
hypotenuse H is tan(X).
However, observe the four quadrants. Our example triangle has
its hypotenuse in the upper-right quadrant [both coordinates
positive]. Horizontal and vertical hypotenuses create line segments
rather than triangles. Also, at least one of the coordinates go
negative in the other three quadrants [upper-left, lower-left,
lower-right].
We proceed by assuming that the coordinates of the vertex, in
Cartesian coordinates, is (cos(X), sin(X)), regardless of where the
vertex is on the unit circle. This immediately leads us to the
Pythagorean identities:
- sin²(X)+cos²(X)=1 [standard; if you memorize only
one, learn this one]
- tan²(X)+1=sec²(X) [divide by cos²(X)]
- 1+cot²(X)=csc²(X) [divide by sin²(X)]
If we interpret undefined as equal to undefined, these identities
hold for arbitrary angles.
Incidentally, the computation of the slope of the hypotenuse H
via tan(X) also works for arbitrary angles. [Recall that an
undefined slope corresponds to a vertical line].
The next point is that the signs of the various trigonometric
functions are controlled by the quadrant the function is evaluated
in. We number the quadrants I through IV [Roman numerals]
counterclockwise, as follows:
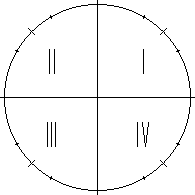 Now, the trigonometric
function signs are controlled by the quadrants as follows:
Now, the trigonometric
function signs are controlled by the quadrants as follows:
- Quadrant I:
- sin(X), csc(X) positive
- cos(X), sec(X) positive
- tan(X), cot(X) positive
- Quadrant II:
- sin(X), csc(X) positive
- cos(X), sec(X) negative
- tan(X), cot(X) negative
- Quadrant III:
- sin(X), csc(X) negative
- cos(X), sec(X) negative
- tan(X), cot(X) positive
- Quadrant IV:
- sin(X), csc(X) negative
- cos(X), sec(X) positive
- tan(X), cot(X) negative
As should be clear, the boundaries between the quadrants do not
behave this way. In fact, they are reference values for the
trigonometric functions. [For ease of memorization, I will put all
of the reference values for the first quadrant and its boundaries
in one place, elsewhere in this document.]
- Boundary between Quadrants I, IV: X is 0° i.e. 0 radians
i.e. 0 gradients; point (1,0)
- sin(0) = 0
- cos(0) = 1
- tan(0) = 0
- cot(0) = undefined
- sec(0) = 1
- csc(0) = undefined
- Boundary between Quadrants I, II:
 i.e. 90° i.e. π/2
radians i.e. 100 gradients
i.e. 90° i.e. π/2
radians i.e. 100 gradients
- sin(
 ) = 1
) = 1
- cos(
 ) = 0
) = 0
- tan(
 ) = undefined
) = undefined
- cot(
 ) = 0
) = 0
- sec(
 ) = undefined
) = undefined
- csc(
 ) = 1
) = 1
- Boundary between Quadrants II, III: 2
 i.e. 180° i.e. π
radians i.e. 200 gradients
i.e. 180° i.e. π
radians i.e. 200 gradients
- sin(2
 ) = 0
) = 0
- cos(2
 ) = -1
) = -1
- tan(2
 ) = 0
) = 0
- cot(2
 ) = undefined
) = undefined
- sec(2
 ) = -1
) = -1
- csc(2
 ) = undefined
) = undefined
- Boundary between Quadrants III, IV: 3
 i.e. 270° i.e. 3π/2
radians i.e. 300 gradients
i.e. 270° i.e. 3π/2
radians i.e. 300 gradients
- sin(3
 ) = -1
) = -1
- cos(3
 ) = 0
) = 0
- tan(3
 ) = undefined
) = undefined
- cot(3
 ) = 0
) = 0
- sec(3
 ) = undefined
) = undefined
- csc(3
 ) = -1
) = -1
Now, let's look at another way to reconstruct the cofunction
identities i.e. the identities relating complementary angles.
 What happens if we reflect the unit circle about the line y=x? We
are swapping the x and y coordinates. That is, (letting X be the
central angle), we are swapping sin(X) and cos(X). We are also
physically reflecting the central angle X to the angle
What happens if we reflect the unit circle about the line y=x? We
are swapping the x and y coordinates. That is, (letting X be the
central angle), we are swapping sin(X) and cos(X). We are also
physically reflecting the central angle X to the angle  -X. So, we find that (here are the cofunction
identities again):
-X. So, we find that (here are the cofunction
identities again):
- sin(
 -X)=cos(X)
-X)=cos(X)
- cos(
 -X)=sin(X)
-X)=sin(X)
- tan(
 -X)=cot(X)
-X)=cot(X)
- cot(
 -X)=tan(X)
-X)=tan(X)
- sec(
 -X)=csc(X)
-X)=csc(X)
- csc(
 -X)=sec(X)
-X)=sec(X)
It is no coincidence that the slope of the line y=x is 1. This
gives a central angle between the line y=x, and the x-axis, of
45° i.e. π/4 i.e. 50 gradients [think
of the 45-45-90 triangle]; note that this is exactly half of a
right angle.
Now, let us consider reflecting the unit circle about the
x-axis:
 Note that the x-coordinate [cos(X)] is unaffected, while the
y-coordinate [sin(X)] is negated. The resulting point is the point
we get from rotating through the angle -X from the angle 0. This
gives the following formulae:
Note that the x-coordinate [cos(X)] is unaffected, while the
y-coordinate [sin(X)] is negated. The resulting point is the point
we get from rotating through the angle -X from the angle 0. This
gives the following formulae:
- sin(-X)=-sin(X) "sin(X) is an odd function"
- cos(-X)=cos(X) "cos(X) is an even function"
- tan(-X)=-tan(X) "tan(X) is an odd function"
- cot(-X)=-cot(X) "cot(X) is an odd function"
- sec(-X)=sec(X) "sec(X) is an even function"
- csc(-X)=-csc(X) "csc(X) is an odd function"
[EXERCISE: derive the last four [tan, cot, sec, and csc versions]
from the first two [sin and cos versions.]
These formulae classify the trigonometric functions into even
functions and odd functions. As you may recall from College
Algebra, even functions are those functions whose value is
unchanged by negating the argument, and odd functions are those
functions whose value is negated by negating the argument.
It is no coincidence that the slope of the x-axis is 0. The
central angle of the x-axis with the x-axis is clearly 0 [degrees,
radians, gradients, it matters not which unit]. 0 is also exactly
half of 0.
Now, let us consider reflecting the unit circle about the y-axis:
 Note that the y-coordinate [sin(X)] is unaffected, while the
x-coordinate [cos(X)] is negated. The resulting point is the point
we get from rotating through the angle -X from the angle 0. This
gives the following formulae:
Note that the y-coordinate [sin(X)] is unaffected, while the
x-coordinate [cos(X)] is negated. The resulting point is the point
we get from rotating through the angle -X from the angle 0. This
gives the following formulae:
- sin(2
 -X)=sin(X)
-X)=sin(X)
- cos(2
 -X)=-cos(X)
-X)=-cos(X)
- tan(2
 -X)=-tan(X)
-X)=-tan(X)
- cot(2
 -X)=-cot(X)
-X)=-cot(X)
- sec(2
 -X)=-sec(X)
-X)=-sec(X)
- csc(2
 -X)=csc(X)
-X)=csc(X)
[EXERCISE: derive the last four (tan, cot, sec, and csc versions)
from the first two (sin and cos versions.)]
It is no coincidence that the slope of the y-axis is undefined.
The central angle of the y-axis with the x-axis is clearly  . This is also exactly half of 2
. This is also exactly half of 2  .
.
Now, we can directly compute the reference values of cos and sin
for 45° i.e. π/4 radians i.e. 50
gradients, i.e. ½ , without using the
45-45-90 reference triangle. 45° is the angle that is its own
complementary angle. Thus,
, without using the
45-45-90 reference triangle. 45° is the angle that is its own
complementary angle. Thus,
- cos(45°) = sin(90° - 45°) = sin(45°)
Substitute the above into the Pythagorean
identity to get
i.e. [solve for cos(45°); we know we need the positive root
because 45° is in the first quadrant, so I can omit ±]
- cos(45°) = 1/
 =
=  /2
/2
We can also directly compute the reference values of cos and sin
for 60°, i.e. π/3 radians, i.e. 200/3
gradients, i.e. [2/3] . To do this, we first
consider inscribing an equilateral hexagon in the unit circle:
. To do this, we first
consider inscribing an equilateral hexagon in the unit circle:
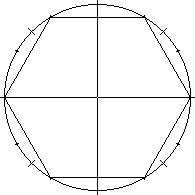 [Just like an equilateral
triangle, an equilateral hexagon has equal lengths for all of its
sides. In general, an equilateral polygon (regardless of how many
sides it has) has equal lengths for all of its sides.]
[Just like an equilateral
triangle, an equilateral hexagon has equal lengths for all of its
sides. In general, an equilateral polygon (regardless of how many
sides it has) has equal lengths for all of its sides.]
Note that the inscribed hexagon can be considered as the
'splicing together' of six equilateral triangles.
[If we draw the line segments from the vertices to the center of
the inscribed hexagon, since the sides have the same length, the
angles as viewed from the center will have the same size.
360/6° = 60°. (The prior two sentences use Euclidean
geometry). We know that the triangle we just created is isosceles,
(two of its sides are radii), so the two angles opposite the radii
have the same size, and add up to 120°: they are both
60°. All three angles are equal. Thus all three sides of the
triangle have equal length. (The very last sentence also uses
Euclidean geometry)]
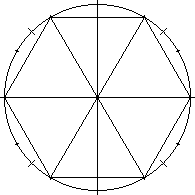 Now, observe that the horizontal side "above the x-axis" is
bisected by the y-axis. Thus, the length of this side in the first
quadrant of the unit circle is ½ [the triangle is equilateral,
so the side being bisected has the length of the radius, i.e. is
length 1]. That is, cos(60°)=½.
Now, observe that the horizontal side "above the x-axis" is
bisected by the y-axis. Thus, the length of this side in the first
quadrant of the unit circle is ½ [the triangle is equilateral,
so the side being bisected has the length of the radius, i.e. is
length 1]. That is, cos(60°)=½.
[The y-axis has an angle of 90° i.e. π/2
radians i.e. 100 gradients. The angle created
by drawing line segments from the vertices of this side, to the
center, starts at 60° and ends at 120°. So, the y-axis is
90° - 60° = 30° into the above angle, which means
the y-axis bisects this angle.]
From the Pythagorean identity, we find
- (½)²+sin²(60°)=1, i.e.
- ¼+sin²(60°)=1
i.e. [solve for sin(60°); we know we need the positive root
because 60° is in the first quadrant, so I can omit ±]
- sin(60°) =
 /2
/2
Since 30° is the complementary angle to 60°, we also have
computed sin(30°) and cos(30°).
How does "wrapping the real number line around the unit circle" work?
The unit circle has a circumference of 2π. "Thus", all trig functions will have the same
value when evaluated 2π radians apart. We
say that all trig functions have a period. [In "stratosphere" math,
this period is arrived at in a very different way.]
The trig function period identities are [X is an angle, n is a
positive integer]:
- sin(X±n[circle]) = sin(X)
- cos(X±n[circle]) = cos(X)
- tan(X±[½] n[circle]) = tan(X)
- cot(X±[½] n[circle]) = cot(X)
- sec(X±n[circle]) = sec(X)
- csc(X±n[circle]) = csc(X)
These identities hold even in the undefined case [if one side is
undefined, they both are.]
To formally demonstrate the n part, I would use natural
induction, which should be buried somewhere in College Algebra. If
you don't recall this term clearly, don't worry about it. However,
I'm only going to explain it for n=1.
We read these from the unit circle immediately:
- sin(X+[circle]) = sin(X)
- cos(X+[circle]) = cos(X)
We use the rewrite of sec(X) and csc(X) in cos(X) and sin(X) to
derive these:
- sec(X+[circle]) = sec(X)
- csc(X+[circle]) = csc(X)
Now, to deal with tan(X) and cot(X), we have to be a little more
clever. For tan(X), write:
- tan(X+[½][circle])
- = sin(X+[½][circle])/cos(X+[½][circle])
- = [-sin(X)]/[-cos(X)]
- = sin(X)/cos(X) = tan(X)
i.e. tan(X+[½][circle])=tan(X). The identity
cot(X+[½][circle]) = cot(X) is similar, but works with the
multiplicative reciprocals throughout.
What are the triangle area formulae?
There are two basic formulae, and one "impractical" one.
"½ base times height"
![The base is the horizontal side of the triangle. The height is the length of the vertical line drawn from the vertex of the triangle not on the base, to the (extended) base. [For the obtuse triangle, the base has been extended in a darker gray.]](grafx/BaseHeightExampleTri.gif)
- (Area)=(½)(length of base)(length of height)
To use this formula, pick one side of the triangle as the "base".
Note its length. Then, draw a perpendicular line segment from the
vertex of the triangle not in the "base", to the "base", and note
this line segment's length (this is the height). [This formula does
work for obtuse triangles. Extend the base to where it would hit
the perpendicular line.].
(height)' is one-half of the area of the rectangle '(base)(height)'.](grafx/BaseHeightExampleTri.gif)
This formula is easily visualized for a right triangle [a
rectangle with a line segment between two opposite vertices gives
two right triangles, both clearly with half the original area since
they are congruent]. It behaves reasonably for line segments [it
gives zero area, which is correct for a line segment; either base
or height is zero for a line segment.]
EXERCISE: learn to use this formula by applying it to the
reference triangles. The 45-45-90 triangle with hypotenuse  should have area ½, and the 30-60-90 triangle with hypotenuse
length 2 should have area
should have area ½, and the 30-60-90 triangle with hypotenuse
length 2 should have area  /2.
/2.
This formula has useful analogies in higher dimensions. The
volume of either a pyramid or a cone, for instance, is given
by:
- (Volume)=(1/3)(area of base)(length of height)
The "obvious generalization" for n-dimensional Euclidean space (n a
positive integer) is
- (n-d hypervolume)=(1/n)(n-1 hypervolume of base)(length of
height)
and for 4-d Euclidean space, English permits a simplification:
- (hypervolume)=(¼)(volume of base)(length of height)
The n-dimensional formula is clearly dimensionally consistent:
using a length unit, both sides have dimension
(length)n. The n-dimensional formula can be directly
computed if one is familiar with iterated integrals (say, from
Calculus III or a decent physics course).
"½ of the product of the lengths of two sides, and the sine
of the included angle"
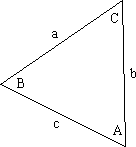
- (Area)=[½](length of side 1)(length of side 2)sin(angle
between sides 1, 2)
- (Area)=[½]absin(C)
- (Area)=[½]acsin(B)
- (Area)=[½]bcsin(A)
We can see this, from the immediately prior formula, by taking side
1 to be the base, side 2 to be the hypotenuse of the right triangle
formed between the [extended, if necessary] base and the height,
and then solving for the height in terms of side 2 and the angle
between sides 1 and 2 [an acute angle of the right triangle we just
constructed].
We get:
- (length of height)=(length of side 2)sin(angle between sides
1,2)

EXERCISE: Learn to use this formula by applying it to the
reference triangles. [The correct areas are the same as
before.]
EXERCISE: Now, learn to use this formula by applying it to the
equilateral triangle with all sides length 2. This triangle is
essentially two copies of the 30-60-90 triangle referred to
earlier, so its area is twice as large —  .
.
I do not know how to generalize the above formula to
n-dimensional Euclidean geometry.
Heron's area formula for a triangle:

- (Area)² = s(s-a)(s-b)(s-c) where s=(a+b+c)/2 and a, b, c
are the lengths of the sides. [Take the positive square root to get
area.]
This formula gives zero when the length of one side is the same as
the length of the other two sides, but will malfunction when one
side has length zero. The Heron referred to here is a Greek
mathematician (B.C.), so the formula can (or should be able to, at
least) be derived in straight Euclidean geometry without
coordinates. However, I have not read this, so I cannot explain it.
EXERCISE: Learn to use this formula by applying it to the
reference triangles, and also to the equilateral triangle with all
sides length 2.
The mathematician Cartan generalized this formula to
n-dimensional Euclidean geometry, using matrix determinants [this
is the determinant of a certain 3x3 matrix]. Cartan's
generalization is definitely beyond the scope of this crash
review.
What is the law of sines?

- sin(A)/a = sin(B)/b = sin(C)/c
Note that the angles A, B, and C are strictly between 0 and 2 in angular measure. This means that solving for
the sine of an angle by the law of sines does not strictly
determine the angle, normally. [It does if the angle is a right
angle; then sin(angle)=1].
in angular measure. This means that solving for
the sine of an angle by the law of sines does not strictly
determine the angle, normally. [It does if the angle is a right
angle; then sin(angle)=1].
If the solved-for sin(angle) is strictly between 0 and 1, then
some work is required to determine the actual angles. The inverse
sine function on a calculator, or spreadsheet, is programmed to
give an acute angle [strictly between 0 and  in angular measure]. However, since the sine of
an angle X is equal to the sine of its supplementary angle 2
in angular measure]. However, since the sine of
an angle X is equal to the sine of its supplementary angle 2 -X [sin(X)=sin(2
-X [sin(X)=sin(2 -X)], the supplementary angle is also a
viable choice.
-X)], the supplementary angle is also a
viable choice.
[EXERCISE: Learn to use the sine law by explicitly writing out
the equalities for the 45-45-90 triangle with hypotenuse  , the
30-60-90 triangle with hypotenuse 2, and the equilateral triangle
with all sides length 2.]
, the
30-60-90 triangle with hypotenuse 2, and the equilateral triangle
with all sides length 2.]
What is
the law of cosines?
This is the generalization of the Pythagorean theorem to non-right
triangles. I'm going to present it "deus ex machina".

- c²=a²+b²-2abcos(C)
- b²=a²+c²-2accos(B)
- a²=b²+c²-2bccos(A)
However, this formula does behave correctly in the extreme cases
[worked for C, others are similar]:
- C=

- C=0
- cos(0)=1. We get:
- c²=a²+b²-2ab, i.e.
- c²=a²-2ab+b², i.e. [this is a standard
reverse-squaring rule from College Algebra]
- c²=(a-b)²
- The last equation is physically correct: if C=0, then the
triangle is really a line segment, and the side c physically has
length |a-b|. This is what the algebra states:
- c²=(a-b)² i.e.
- |c|=|a-b| i.e. [c is guaranteed to be non-negative, since it
represents a physical length]
- c=|a-b|
- C=2

- cos(2
 )=-1. We get:
)=-1. We get:
- c²=a²+b²+2ab, i.e.
- c²=a²+2ab+b², i.e. [this is a standard
reverse-squaring rule from College Algebra]
- c²=(a+b)²
- The last equation is physically correct: if C=2
 , then the triangle is really a line segment, and
the side c physically has length a+b. This is what the algebra
states:
, then the triangle is really a line segment, and
the side c physically has length a+b. This is what the algebra
states:
- c²=(a+b)² i.e.
- |c|=|a+b| i.e. [a, b, c are all guaranteed to be non-negative,
since they represent physical lengths]
- c=a+b
[EXERCISE: Learn to use the cosine law by explicitly writing out
the equalities for the 45-45-90 triangle with hypotenuse , the
30-60-90 triangle with hypotenuse 2, and the equilateral triangle
with all sides length 2.]
What are
the angle sum, difference, and/or doubling formulae?
I'm going to present these "deus ex machina". [The least painful
method, to me, is 2x2 matrices -- inappropriate here.]
The basic angle sum formulae are [A,B are arbitrary angles
here]:
- sin(A+B)=sin(A)cos(B)+sin(B)cos(A)
- cos(A+B)=cos(A)cos(B)-sin(A)sin(B)
The other four trigonometric functions can be recovered from these
two. Note: the tan(A+B) formula has a relatively clean version
(assuming neither tan(A) nor tan(B) is undefined):
- tan(A+B)=[sin(A)cos(B)+sin(B)cos(A)]/[cos(A)cos(B)-sin(A)sin(B)]
- =[tan(A)+tan(B)]/[1-tan(A)tan(B)] [we divided both top and
bottom by cos(A)cos(B)]
That is,
- tan(A+B)=[tan(A)+tan(B)]/[1-tan(A)tan(B)]
Now, using A-B = A+(-B), we can use the even-odd identities to
easily derive the following:
- sin(A-B)=sin(A)cos(B)-sin(B)cos(A)
- cos(A-B)=cos(A)cos(B)+sin(A)sin(B)
- tan(A-B)=[tan(A)-tan(B)]/[1+tan(A)tan(B)]
Also, by setting A=B, we get the following double-angle formulae:
- sin(2A)=2sin(A)cos(A)
- cos(2A)=cos²(A)-sin²(A)
- tan(2A)=2tan(A)/[1-tan²(A)]
[EXERCISES: Learn to use these formulae with the reference values
we already have: 0°, 30°, 45°, 60°, and
90°. Namely: try A=0° [should reduce to trigonometric
function of B or -B, respectively] and B=0° [trigonometric
function of A]. Also, try 2*0°=0°, 2*45°=90°,
2*30°=60°, and 30°+60° = 90°. Ranging into
the second quadrant: try 90°+(another reference angle),
2*60° = 120°, and 2*90° = 180°. The tangent
identities should not be usable when one of the angles is a right
angle.]
Note: several entries in Trigonometry Survival 201 are/will be
based on this.
What are
the angle-halving formulae?
The angle-halving formulae are easily derived from the Pythagorean Identity and the formula for
cos(2A). In general, we need to know which quadrant the angle A/2
is in to decide on the correct sign.
Observe:
- 1+cos(2A)=[cos²(A)+sin²(A)]+[cos²(A)-sin²(A)]=2cos²(A)
- 1-cos(2A)=[cos²(A)+sin²(A)]-[cos²(A)-sin²(A)]=2sin²(A)
In both cases, we can isolate the trigonometric function on the RHS
[right-hand side] by dividing by 2, then taking the square root.
This yields:
- cos(A)=±SQRT[(1+cos(2A))/2]
- sin(A)=±SQRT[(1-cos(2A))/2]
Rename A as A/2 to get:
- cos(A/2)=±SQRT[(1+cos(A))/2]
- sin(A/2)=±SQRT[(1-cos(A))/2]
If we know which quadrant the angle A/2 is in, we can decide on the
correct sign in the above formulae.
We also have [exercise: derive the following]:
- tan(A/2)=±SQRT[(1-cos(A))/(1+cos(A))]
The Pythagorean identity allows two easy rewrites of the above
[observe that the ± negates the usefulness of | |, here]:
- tan(A/2)=±|sin(A)|/(1+cos(A))=±sin(A)/(1+cos(A))
- tan(A/2)=±(1-cos(A))/|sin(A)|=±(1-cos(A))/sin(A)
[EXERCISES: Learn to use the above with reference values. Namely:
0° = [½]0°,
30° = [½]60°, 45° = [½]90°,
60° = [½]120°, and 90° = [½]180°. For
the tangent identities, both sides should be undefined for the
90° case.]
What are the
trig(onometric) sum and difference formulae?
What are the trig(onometric) product formulae?
These formulae may be derived from the angle sum and difference
formulae. We have:
- sin(A+B)+sin(A-B)=2sin(A)cos(B)
- sin(A+B)-sin(A-B)=2sin(B)cos(A)
- cos(A+B)+cos(A-B)=2cos(A)cos(B)
- cos(A+B)-cos(A-B)=2sin(A)sin(B)
- tan(A+B)+tan(A-B)=2(tan(A)[1+tan2(B)])/[1-tan2(A)tan
2(B)]
- tan(A+B)-tan(A-B)=2(tan(B)[1+tan2(A)])/[1-tan2(A)tan
2(B)]
All are trig(onometric) sum or difference formulae. The first four
are also product formulae.
EXERCISE: Derive these from the angle sum and difference
formulae, as follows:
- Set X=A+B and Y=A-B .
- Substitute in the angle sum and difference formulae for the
affected functions, and simplify.
- Solve for A and B in terms of X and Y, and then replace A, B
with their expressions in X, Y.
EXERCISE: Numerically use the sum and difference identities for
X=A+B, Y=A-B where A, B are reference angles. The tangent ones will
break down when 90° is A, B, X, or Y.
EXERCISE: Numerically use the product identities for A=(X+Y)/2,
B=(X-Y)/2 where X, Y are reference angles.
Wait! I'm not completely sure how to solve for A and B in terms of
X and Y!
Until I get a College Algebra page going, here's a quick summary
on how to solve systems of linear equations. (This domain can use
several.) [While not all systems of linear equations are
solvable, the one we want to is solvable.]
- Substitution
- We hope that by cleverly adding multiples of pairs of
equations, we can get equations with reasonably isolated variables.
This works fairly well with two variables.
- How this works in practice:
- X=A+B, Y=A-B.
- To solve for A, eliminate B from the resulting sum and then
solve. Since 1+(-1)=0, we simply add both equations: X+Y=2A.
Dividing by 2 yields (X+Y)/2=A.
- To solve for B, eliminate A from the resulting sum and then
solve. Since 1+(-1)*1=0, we subtract Y=A-B from X=A+B: X-Y=2B.
Dividing by 2 yields (X-Y)/2=B.
- Gaussian Elimination (named after Gauss, the
mathematician)
- Taking variables from left to right (in our case, A, then B):
- Pick a linear equation using the "leading variable". If this
variable's coefficient is not 1, divide the equation by this
coefficient. This equation is now the "topmost equation".
- By adding a suitable multiple of the "topmost equation" to the
other equations, remove A from the resulting equations.
- We are now done with the "topmost equation". Set it aside.
- When the only equations left have a multiple of a single
variable equal to a constant, solve those variables. Then replace
those variables in the equations that have been set aside. Repeat
until all variables have been explicitly solved.
- How this works in practice:
- X=A+B, Y=A-B: A is "leading variable". Both X=A+B and Y=A-B
have coefficient 1 for A.
- However, the multiple of the "topmost equation" I am
subtracting is 1[=1/1; numerator is from the equation I am
subtracting from, denominator is from the "topmost equation". I
arbitrarily choose my topmost equation to be Y=A-B.
- We subtract Y=A-B (i.e. 1*[Y=A-B]) from X=A+B to get X-Y=2B.
- We solve for B: B=(X-Y)/2.
- We then subsitute this into the "topmost equation" X=A+B, getting X=A+(X-Y)/2
- Isolating A, we end up at (X+Y)/2=A.
- Cramer's Rule: This is theoretically interesting, since it
directly informs you when the system of linear equations does not
have a unique solution. However, it requires the introduction of
even more terminology. I won't cover it in this refresher.
Angle
classifications
- Acute -- strictly between 0 and

- strictly between 0 and 90°
- strictly between 0 and π/2 radians
- strictly between 0 and 100 gradients
- Right --

- exactly 90°
- exactly π/2 radians
- exactly 100 gradients
- Obtuse -- strictly between
 and 2
and 2 
- strictly between 90 and 180°
- strictly between π/2 and π radians
- strictly between 100 and 200 gradients
- Straight Line i.e half a circle -- 2

- 180°
-
π radians
- 200 gradients
Angle
relations
For angles X, Y:
- complementary: the sum of the two angles is

- X+Y = 90°
- X+Y = π/2 radians
- X+Y = 100 gradients
- supplementary: the sum of the two angles is 2
 i.e half a circle.
i.e half a circle.
- X+Y = 180°
- X+Y = π radians
- X+Y = 200 gradients
Cofunction relations
For an angle X:
- sin(
 -X)=cos(X)
-X)=cos(X)
- sin(90° -X)=cos(X)
- sin(π/2 radians-X)=cos(X)
- sin(100 gradients-X)=cos(X)
- cos(
 -X)=sin(X)
-X)=sin(X)
- cos(90° -X)=sin(X)
- cos(π/2 radians-X)=sin(X)
- cos(100 gradients-X)=sin(X)
- tan(
 -X)=cot(X)
-X)=cot(X)
- tan(90° -X)=cot(X)
- tan(π/2 radians-X)=cot(X)
- tan(100 gradients-X)=cot(X)
- cot(
 -X)=tan(X)
-X)=tan(X)
- cot(90° -X)=tan(X)
- cot(π/2 radians-X)=tan(X)
- cot(100 gradients-X)=tan(X)
- sec(
 -X)=csc(X)
-X)=csc(X)
- sec(90° -X)=csc(X)
- sec(π/2 radians-X)=csc(X)
- sec(100 gradients-X)=csc(X)
- csc(
 -X)=sec(X)
-X)=sec(X)
- csc(90° -X)=sec(X)
- csc(π/2 radians-X)=sec(X)
- csc(100 gradients-X)=sec(X)
Supplementary angle
relations
For an angle X:
- sin(2
 -X)=sin(X)
-X)=sin(X)
- sin(180° -X)=sin(X)
- sin(π radians-X)=sin(X)
- sin(200 gradients-X)=sin(X)
- cos(2
 -X)=-cos(X)
-X)=-cos(X)
- cos(180° -X)=-cos(X)
- cos(π radians-X)=-cos(X)
- cos(200 gradients-X)=-cos(X)
- tan(2
 -X)=-tan(X)
-X)=-tan(X)
- tan(180° -X)=-tan(X)
- tan(π radians-X)=-tan(X)
- tan(200 gradients-X)=-tan(X)
- cot(2
 -X)=-cot(X)
-X)=-cot(X)
- cot(180° -X)=-cot(X)
- cot(π radians-X)=-cot(X)
- cot(200 gradients-X)=-cot(X)
- sec(2
 -X)=-sec(X)
-X)=-sec(X)
- sec(180° -X)=-sec(X)
- sec(π radians-X)=-sec(X)
- sec(200 gradients-X)=-sec(X)
- csc(2
 -X)=csc(X)
-X)=csc(X)
- csc(180° -X)=csc(X)
- csc(π radians-X)=csc(X)
- csc(200 gradients-X)=csc(X)
Basic
trigonometric reference tables
|
sin |
cos |
tan |
cot |
sec |
csc |
| 0° |
0 |
1 |
0 |
undefined |
1 |
undefined |
| 30° |
½ |
 /2 /2 |
 /3 /3 |
 |
(2 )/3 )/3 |
2 |
| 45° |
 /2 /2 |
 /2 /2 |
1 |
1 |
 |
 |
| 60° |
 /2 /2 |
½ |
 |
 /3 /3 |
2 |
(2 )/3 )/3 |
| 90° |
1 |
0 |
undefined |
0 |
undefined |
1 |
Exercise: convert the angles to radians. If you plan to use
gradients, also convert the angles to gradients.
If you find the above table difficult to memorize for sin and
cos, my ex-fianceé suggests this alternative table [it uses
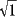 =1 and
=1 and 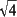 =2]:
=2]:
|
0° |
30° |
45° |
60° |
90° |
| sin |
0/2 |
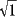 /2 /2 |
 /2 /2 |
 /2 /2 |
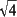 /2 /2 |
| cos |
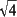 /2 /2 |
 /2 /2 |
 /2 /2 |
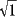 /2 /2 |
0/2 |
If you find this alternative table convenient, you may want to
check that the entries that look different, do algebraically reduce
to those in the first table.
Reference
values -- 15° and 75° i.e. π/12
and 5π/12 radians i.e. 100/6 and 500/6
gradients
Exercise: verify that these tables are correct:
|
sin |
cos |
tan |
cot |
sec |
csc |
| 15° |
[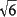 - - ]/4 ]/4 |
[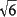 + + ]/4 ]/4 |
2- |
2+ |
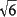 - - |
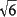 + + |
| 75° |
[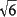 + + ]/4 ]/4 |
[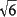 - - ]/4 ]/4 |
2+ |
2- |
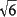 + + |
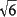 - - |
Suggestions: Note that 15° is computable either with the
half-angle or the difference-angle formula from the standard
reference table. Use both of these methods. Also, 75° can be
computed by the sum formula from the standard reference table; use
this method. Once you are confident that these tables are correct,
and if you want more practice with the angle sum, difference,
halving, and doubling formulae, use these additional reference
values in combination with the earlier ones [0°, 30°,
45°, 60°, and 90°, i.e. the standard table].
[Exercise: translate everything into radians. If you plan to use
gradients, also translate everything into gradients.]
Reference values -- 18°,
36°, 54°, and 72° i.e. π/10,
π/5, 3π/10, and
2π/5 radians i.e. 20, 40, 60, and 80
gradients
EXERCISE: Verify that these tables are correct:
|
sin |
cos |
tan |
cot |
| 18° |
[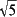 -1]/4 -1]/4 |
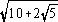 /4 /4 |
[5-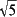 ] ]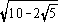 /20 /20 |
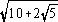 [ [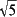 +1]/4 +1]/4 |
| 36° |
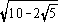 /4 /4 |
[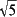 +1]/4 +1]/4 |
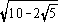 [ [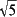 -1]/4 -1]/4 |
[5+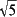 ] ]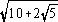 /20 /20 |
| 54° |
[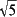 +1]/4 +1]/4 |
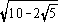 /4 /4 |
[5+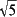 ] ]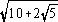 /20 /20 |
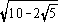 [ [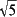 -1]/4 -1]/4 |
| 72° |
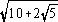 /4 /4 |
[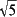 -1]/4 -1]/4 |
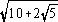 [ [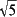 +1]/4 +1]/4 |
[5-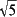 ] ]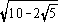 /20 /20 |
|
sec |
csc |
| 18° |
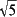 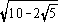 /5 /5 |
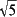 +1 +1 |
| 36° |
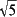 -1 -1 |
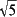 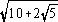 /5 /5 |
| 54° |
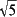 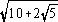 /5 /5 |
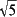 -1 -1 |
| 72° |
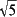 +1 +1 |
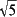 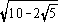 /5 /5 |
Suggestions: First, let X be an angle such that 5X works out to
be 0, 1, 2, 3, or 4 full circles.
[That is, we are directly interested in 72°, 144°,
216°, or 288°. I also included 0°, but that is a
standard reference value. We will recover:
- 18° from 72° and the cofunction identities
- 36° from 144° and the supplementary angle
identities
- 54° from 36° and the cofunction identities
It may provide some intuition about the following equations to
subtract 1 circle off 216° [-144°] and 288°
[-72°].]
Next, use the angle addition
formulae to rewrite in terms of sin(X) and cos(X)
- sin(5X)=0
- cos(5X)-1=0 [a convenient rewrite of cos(5X)=1, for this
problem]
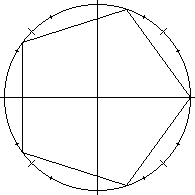
These are the equations that describe an inscribed equilateral
pentagon. They are solvable using nothing more than the
quadratic formula(!), and what we already are supposed to know.
This would occur to me from sin(X) being an (algebraically) odd function, combined with the angle
comments above:
sin(0°)=0, so we can factor sin(X) out of our expanded
version of sin(5X)=0. Then, use the Pythagorean identity to replace
cos²(X) with 1-sin²(X). Expand the results. This should
give a quartic in sin(X) [oops], which is also a quadratic in
sin²(X) [great]. Use the quadratic formula to solve for
sin²(X). Then take square roots on the solutions we get for
sin²(X); we need both the positive and negative roots. One of
these root sets is for 72° and -72°, and the other one is
for 144° and -144°.

Geometrically, the larger positive root goes with 72°, and
the smaller positive root goes with 144°. Solve for cosine of
72° and 144° with the Pythagorean
identity [be sure to use the quadrants to force the correct sign].
Then fill in the table as summarized initially.
Also: when completing the table, tan(18°) and tan(54°)
[and their corresponding cofunction values, cot(72°) and
cot(36°)] are technically difficult to algebraically compute
directly from the sine and cosine values. [The denominator needs
two stages to cancel out correctly.] I tried that three times in a
row, and got three different answers, all of them wrong. The method
I used for the table was to compute cot(18°) and cot(54°)
respectively, and then take the multiplicative inverse
algebraically to get tan(18°) and tan(54°).
Instant
numerical trigonometric tables for sin, cos, and tan near
0
This isn't really "fair", since it relies on the "stratosphere"
math approach. The first mention of the basis for this,
traditionally, is in the middle of a Calculus series [business or
conventional].
However, it is very practical. (Especially if you plan to use
trigonometry in an engineering course.) I'm going to present how
the result is arrived at in just enough detail, that those readers
who actually know the relevant material will be able to see that
I'm doing it right.
The key point is: for an angle X with radian measure
0<X<1, we have
- sin(X)<X, and furthermore X-sin(X)<X³/6
- cos(X)>1-X², and furthermore
cos(X)-1+X²<(X4)/24
[If you know what a power series is, and the alternating series
test for convergence, you will immediately recognize what I'm
doing. If not -- well, I said this wasn't "fair". Put these
equations and inequalities into a spreadsheet to see why the above
is plausible. If you don't have access to a spreadsheet, then use a
calculator. If you don't have even that, at least do it for the
numbers 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9.]
For three decimal place accuracy (the least we are interested
in, for practical purposes), we need to control the error to less
than 5*10-4 i.e. [½]10-3. This error
term is:
- for sin(X), X³/6
- for cos(X), (X4)/24
Now, let's solve for X:
- sin(X)
- X³/6<5*10-4 i.e.
- X³<30*10-4 i.e.
- X³<3*10-3 i.e.
- X<[31/3]/10 which is between 0.144 and 0.145
- cos(X)
- (X4)/24<5*10-4 i.e.
- X4<120*10-4 i.e. [yes, there's a
reason I'm not reducing here!]
- X<[1201/4]/10 which is between 0.330 and
0.331
That is, for X in radians:
- when 0<X<0.144, sin(X)=X to three decimal places
- when 0<X<0.330, cos(X)=1-X² to three decimal
places
What if you want the "instant trig table" to more decimal places?
Just work the above bound calculations with 5*10-(number of
decimal places+1) instead of 5*10-4. Note that at
the final stage, I took the decimal my TI-36SX Solar calculator
gave out, and found the three-decimal place numbers that bracketed
it. For a different number of decimal places, bracket the result
with decimals to as many places as you need precision.
Computing tan(X) and sec(X) from the results of this "instant
trig table" will give reasonably accurate numerical results.
Computing cot(X) and csc(X) will not work reasonably "near 0"; in
general, you cannot get more significant digits out than you put
in, and sin(X) will lose significant digits as X ends up near 0.
This means you are dividing a large number by a small, imprecise
number, which will not give reasonable numerical results.
[The zero decimal places between the decimal point and the first
non-zero digit are "lost significant digits". For example,
sin(0.021)=0.021 to three decimal places -- but there are only two
significant digits.]
AMAZON.COM® is the registered trademark of Amazon.com, Inc.
Opinions, comments, criticism, etc.? Let me know about it.
Return to the Math page, or the Iskandria wargame requirements page, or the main page.


![The hatch marks for sin(x)=1 are at pi/2 and -3pi/2. The hatch marks for sin(x)=-1 are at -pi/2 and 3pi/2. Sin(x)=0 [intersects the x-axis] at ±2pi, ±pi, and 0](grafx/RefSin.gif)

![]() in the rest of this crash review; this is
not standard notation. An implicit exercise will be
translating 2
in the rest of this crash review; this is
not standard notation. An implicit exercise will be
translating 2![]() to angular measure [degrees, radians,
and/or gradients.].
to angular measure [degrees, radians,
and/or gradients.].
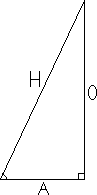 the generic right triangle, and
the generic right triangle, and  the unit circle.
the unit circle.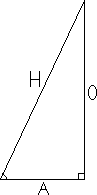 Given a
right triangle, the trig function values for the two acute angles
[angles smaller than a right angle] can be computed without knowing
the angles. I prefer to remember the formulae this way [X is an
angle]:
Given a
right triangle, the trig function values for the two acute angles
[angles smaller than a right angle] can be computed without knowing
the angles. I prefer to remember the formulae this way [X is an
angle]:![]() -X is complementary to X.
-X is complementary to X.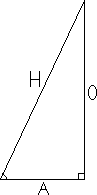 For instance, the angle in the upper right-hand corner is
complementary to, i.e. the complement of, the marked angle in the
lower left-hand corner.
For instance, the angle in the upper right-hand corner is
complementary to, i.e. the complement of, the marked angle in the
lower left-hand corner.![]() - X is supplementary to
the angle X. To get an intuition for this, draw a unit circle with
the horizontal axis.. Draw an arbitrary radius from the center to
somewhere on the unit circle. The two angles formed between the
radius, and the horizontal axis, are supplementary.
- X is supplementary to
the angle X. To get an intuition for this, draw a unit circle with
the horizontal axis.. Draw an arbitrary radius from the center to
somewhere on the unit circle. The two angles formed between the
radius, and the horizontal axis, are supplementary. When we put A=1=O and H=
When we put A=1=O and H=![]() into the generic right triangle, we get:
into the generic right triangle, we get: We now have a hypotenuse of length 2, one leg of length 1 [from
bisecting the horizontal side], and one side with length
We now have a hypotenuse of length 2, one leg of length 1 [from
bisecting the horizontal side], and one side with length ![]() [from the bisecting line].
[from the bisecting line]. Think of it as the set of
possible endpoints for a length 1 hypotenuse H, with one endpoint
of H fixed at the origin. We can construct generic right triangles
with hypotenuse 1 in it. Pick a point on the circumference, draw a
line segment from it to the origin, and then draw a perpendicular
line segment down to the x-axis.
Think of it as the set of
possible endpoints for a length 1 hypotenuse H, with one endpoint
of H fixed at the origin. We can construct generic right triangles
with hypotenuse 1 in it. Pick a point on the circumference, draw a
line segment from it to the origin, and then draw a perpendicular
line segment down to the x-axis. Notice that
the coordinates of the vertex, in Cartesian coordinates, is
(cos(X), sin(X)), where X is the central angle. The horizontal side
(on the x-axis) is A, and the vertical side (parallel to the
y-axis) is O. The radius (length 1) is H. The slope of the
hypotenuse H is tan(X).
Notice that
the coordinates of the vertex, in Cartesian coordinates, is
(cos(X), sin(X)), where X is the central angle. The horizontal side
(on the x-axis) is A, and the vertical side (parallel to the
y-axis) is O. The radius (length 1) is H. The slope of the
hypotenuse H is tan(X). Now, the trigonometric
function signs are controlled by the quadrants as follows:
Now, the trigonometric
function signs are controlled by the quadrants as follows: What happens if we reflect the unit circle about the line y=x? We
are swapping the x and y coordinates. That is, (letting X be the
central angle), we are swapping sin(X) and cos(X). We are also
physically reflecting the central angle X to the angle
What happens if we reflect the unit circle about the line y=x? We
are swapping the x and y coordinates. That is, (letting X be the
central angle), we are swapping sin(X) and cos(X). We are also
physically reflecting the central angle X to the angle ![]() -X. So, we find that (here are the cofunction
identities again):
-X. So, we find that (here are the cofunction
identities again): Note that the x-coordinate [cos(X)] is unaffected, while the
y-coordinate [sin(X)] is negated. The resulting point is the point
we get from rotating through the angle -X from the angle 0. This
gives the following formulae:
Note that the x-coordinate [cos(X)] is unaffected, while the
y-coordinate [sin(X)] is negated. The resulting point is the point
we get from rotating through the angle -X from the angle 0. This
gives the following formulae: Note that the y-coordinate [sin(X)] is unaffected, while the
x-coordinate [cos(X)] is negated. The resulting point is the point
we get from rotating through the angle -X from the angle 0. This
gives the following formulae:
Note that the y-coordinate [sin(X)] is unaffected, while the
x-coordinate [cos(X)] is negated. The resulting point is the point
we get from rotating through the angle -X from the angle 0. This
gives the following formulae:![]() . This is also exactly half of 2
. This is also exactly half of 2 ![]() .
.![]() , without using the
45-45-90 reference triangle. 45° is the angle that is its own
complementary angle. Thus,
, without using the
45-45-90 reference triangle. 45° is the angle that is its own
complementary angle. Thus, [Just like an equilateral
triangle, an equilateral hexagon has equal lengths for all of its
sides. In general, an equilateral polygon (regardless of how many
sides it has) has equal lengths for all of its sides.]
[Just like an equilateral
triangle, an equilateral hexagon has equal lengths for all of its
sides. In general, an equilateral polygon (regardless of how many
sides it has) has equal lengths for all of its sides.] Now, observe that the horizontal side "above the x-axis" is
bisected by the y-axis. Thus, the length of this side in the first
quadrant of the unit circle is ½ [the triangle is equilateral,
so the side being bisected has the length of the radius, i.e. is
length 1]. That is, cos(60°)=½.
Now, observe that the horizontal side "above the x-axis" is
bisected by the y-axis. Thus, the length of this side in the first
quadrant of the unit circle is ½ [the triangle is equilateral,
so the side being bisected has the length of the radius, i.e. is
length 1]. That is, cos(60°)=½.![The base is the horizontal side of the triangle. The height is the length of the vertical line drawn from the vertex of the triangle not on the base, to the (extended) base. [For the obtuse triangle, the base has been extended in a darker gray.]](grafx/BaseHeightExampleTri.gif)
(height)' is one-half of the area of the rectangle '(base)(height)'.](grafx/BaseHeightExampleTri.gif)
![]() should have area ½, and the 30-60-90 triangle with hypotenuse
length 2 should have area
should have area ½, and the 30-60-90 triangle with hypotenuse
length 2 should have area ![]() /2.
/2.

![]() .
.

![]() in angular measure]. However, since the sine of
an angle X is equal to the sine of its supplementary angle 2
in angular measure]. However, since the sine of
an angle X is equal to the sine of its supplementary angle 2![]() -X [sin(X)=sin(2
-X [sin(X)=sin(2![]() -X)], the supplementary angle is also a
viable choice.
-X)], the supplementary angle is also a
viable choice.![]() , the
30-60-90 triangle with hypotenuse 2, and the equilateral triangle
with all sides length 2.]
, the
30-60-90 triangle with hypotenuse 2, and the equilateral triangle
with all sides length 2.]
![]() =1 and
=1 and ![]() =2]:
=2]:
