The science fantasy behind Faster-Than-Light anything

I will use the acronym FTL [faster than light] freely in this page.

Larry Niven, in "N-Space", presents an excellent explanation of why any sort of interstellar politics almost requires FTL travel and communication. I need this politics for my science fantasy.

The physics in Iskandria's universe is forgiving: all of the classic FTL travel paradigms can be constructed.

Hyperdrive: Lost In Hyperspace

Teleportation (and how to keep it from turning into hyperdrive)

Warp Drive

Exorcising time travel from the universe

• For simplicity, let's consider a drive that travels at twice the speed of light. The question is, "which reference frame?" The idea is that by traveling at twice the speed of light from the viewpoint of Earth, and then traveling at twice the speed of light with respect to (say) some cosmic ray, we could end up in the past compared to when we started. I will not go into all of the standard horrors this entails. These horrors are definitely worth excluding.
• Note, however, that the above argument falls apart if there is a physically preferred way of measuring FTL travel. This amounts to an "FTL ether", by analogy to the search for "ether" in a late 1800's attempt to reconcile electromagnetic theory [Maxwell's equations] and the conventional Newtonian mechanics.
• Maxwell's equations are not preserved by the coordinate transformations of classical mechanics. They are preserved by the Lorentz transformations of General Relativity.
• Newton's Three Laws are preserved under Lorentz transformations. This is not intuitive. In fact, Newton formulated his laws to account for the possibility that the mass of an object might depend on its velocity.
• It was known, in 1876, that classical mechanics applied to Maxwell's equations predicted no magnetism. Thus, the telegraph (around before 1876) was direct proof that classical mechanics was not completely correct -- just a good approximation in the Earth-normal physics regime. [This is in some chemistry textbook in one of the Johnson County, KS libraries. I read it in 1988 or 1989.]
• The "ether" was an attempt to impose a preferred reference frame for electromagnetism. Such a preferred frame would make it impossible to apply classical mechanics to Maxwell's equations.
• The Michelson-Morley experiment used a rapidly-spinning series of mirrors to measure the speed of light. It was thought that at different points in the Earth's orbit, the Earth's motion relative to the "ether" [the correct frame of reference for electromagnetism] would change the measured velocity of light. No such change was measurable.
• Mathematically, a physically preferred way of measuring FTL travel would immediately result in a preferred factorization of space-time into space and time. I don't have access to physical evidence that either requires, or excludes, such a factorization. If you know of any evidence relevant to this, please email me with a description of this evidence. This preferred factorization would have no obvious effects on how to do computational General Relativity efficiently.
• An "FTL ether" prevents time travel by guaranteeing that no sequence of FTL travels can end in the past relative to the starting point. It does not affect most phenomena operating slower-than-light.

Hyperdrive: Lost In Hyperspace

The following commentary does not depend on the 'exorcism of time travel' comment, above: changes in coordinate systems merely alter the apparent FTL speed, not the fact it is faster than FTL.

• For a finite FTL speed v, the Lorentz contraction factor 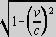is a purely imaginary complex number.
• EXERCISE: We are taking the square root of a negative number.
• A mathematically clean way to interpret this is that a hyperdrive travels at right angles to the universe in all four coordinates -- when departing and arriving. One should think of "going out a certain distance", then "returning to a different place in space-time". My motivation for this is the coordinate expression of 4-momentum in General Relativity.
• Unfortunately, an error in the return position that cannot be measured, results in completely missing the universe we want to return to.

Teleportation

• Both the departure point, and the arrival point, will radiate gravity waves.
• I haven't researched whether this can be worked to preserve the locality principle. Then again, the locality principle may not be that meaningful at Planck time scales.
• In the absence of a preferred space-time factorization for FTL phenomena, almost all coordinate-changes turn teleportation into de-facto hyperdrive (with the usual problems).

Warp Drive

• Anders' links & mirror [FTL section] to a metadesign for a warp drive -- and an attempt to use Quantum Mechanics+General Relativity to show it can't be built.
• Quantum Gravity has not been formulated -- yet. The attempt may, or may not, be successful.
• Observe that this metadesign assumes a preferred reference frame for the calculations, in spite of the construction being for two space-like related points. I have not seen a demonstration that warp drives require a preferred space-time factorization for FTL.

• The gravitational fields around a warp drive are not to be mocked.
• The energy required to create these gravitational fields is also not to be mocked.
• While wormholes are related, these shortcuts do not cause FTL effects.

Return to Iskandria, or the main page.