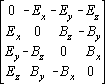Quantum Mechanics and General Relativity: Incomplete Working Notes
This isn't going to be anywhere near comprehensive for some time: I have decided to seriously
study this subject (something I didn't really have time for at K-State).
I am currently studying from the following textbooks:
| | One of the few General Relativity textbooks that uses
differential manifolds rather than coordinates as the primary viewpoint for the subject. |
| This textbook avoids measure theory. |
If you don't have a decent understanding of at least elementary differential equations and a
three-semester calculus series, these notes will become techno-jargon practically immediately....
While I am going to pay attention to some notational details, I do not intend this to be a
mathematically rigorous presentation.
Reference data
 National Institute of Standards and Technology This should have most physics constants in it &endash;
somewhere....
National Institute of Standards and Technology This should have most physics constants in it &endash;
somewhere....
A vastly incomplete selection of Web resources
Indeed. No links have been implemented yet.
Topical Index
Basic Terminology
The (Lorentz) metric tensor
Physical Formulae
Einstein-de Broglie equations
Lorentz and Poincar´ transforms
Gravity via a uniformly accelerating rocket
Free-fall in a uniform gravity field
Normalization of quantum state functions
Electromagnetism in a tangent Minkowski space
Basic terminology
The Cartesian coordinate representation of a vector in:
- ℝ4 is (t,x,y,z) i.e. (x0,x1,x2,x3) [with standard basis vectors e0, e1, e2, e3]
- ℝ3 is (x,y,z) i.e. (x1,x2,x3) [with standard basis vectors e1, e2, e3 i.e. i, j, k]
The Cartesian coordinate representation of a 1-form over:
- ℝ4 is a0dx0+a1dx1+a2dx2+a3dx3
- ℝ3 is a1dx1+a2dx2+a3dx3
We prefer to interpret the gradient df as a 1-form, rather than as a vector:
- df :=
(¶f/¶x0)dx0+(¶f/¶x1)dx1+(¶f/¶x2)dx2+(¶f/¶x3)dx3 i.e.
- df :=
¶0f dx0+¶1f dx1+¶2f dx2+¶3f dx3 i.e.
- df :=
f0dx0+f1dx1+f2dx2+f3dx3
Over a region of space-time with curvature i.e. gravity smaller than we care to measure, we can
represent that region of space-time by a region in ℝ4 without concern. [This is when special relativity
calculations suffice.] The coordinate t is said to be the time-coordinate. The coordinates x, y, and
z are said to be space coordinates. We say this representation by ℝ4 is a Lorentz (reference)
frame. We may loosely use notation, and think of dt as dx0, dx as dx1, dy as dx2, and dz as dx3.
To "geometrize" units, the following constants must have the given values:
- The speed of light c:=1
- Newton's gravitational constant G:=1
- Boltzmann's constant k:=1
Assuming seconds for the time unit, Earth's surface gravity g has an interesting geometrization:
- g = 9.801 m/sec2 [to 4 significant digits]
- = 3.264·10-9 light-sec/sec2 [to 4 significant digits]
- = 1.040·10-9·p light-sec/sec2 [to 4 significant digits]
- = [26/25]·10-9·p light-sec/sec2
Planck's constant takes two forms in Quantum mechanics:
- h: very roughly, 6.626·10-34 J·sec
- h:=h/(2p) [this should be an "h" with a slash through the upper part]
Within a Lorentz frame:
- Mass is denoted by m.
- Frequency is denoted by n.
- Wavelength is denoted by l.
- The conventional velocity [i.e. 3-velocity] vector v is defined in coordinates as:
- vj = dxj/dt, j=1..3
- This should look familiar from classical physics.
- In Einstein summation notation, this is: (dxj)ej
- With the summation sign, this is: å (dxj)ej
- The conventional momentum [i.e. 3-velocity] vector p is defined as p := mv .
- Proper time t is the time measured by a (theoretical) clock that satisifies v(t)=0 for all time
coordinates t.
- The 4-velocity vector u has components:
- u0 = dt/dt = 1/
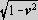
- uj = dxj/dt = (dxj/dt)/
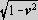 , j=1..3
, j=1..3
- The 4-momentum vector r is defined as r := mu. It has coordinate
representation (E,px,py,pz) in any fixed Lorentz frame in Cartesian coordinates.
- The charge density-current 4-vector has components (r,jx,jy,jz) in any fixed Lorentz frame in Cartesian coordinates.
Here, r is charge density, and the j components are current components as viewed in space.
In all cases, we may use subscripts to distinguish between various objects' properties.
To "de-geometrize units", use the following substitutions, where c is the speed of light in the
chosen non-geometric unit system (using definitions as above):
- replace m by mc2
- replace v by v/c
- replace p by cp
- u and r do not appear to have clean substitutions.
I follow Wheeler in not treating the time coordinate as a special case: replace t by ct, not by ict.
I will consider a state function Y for a quantum-mechanical system to be a restriction of a function
(space-time manifold) ® ℂ. For a Lorentz frame with a specific coordinate chart,
this can be rewritten as the more familiar form Y(x,t): ℝ4 ® ℂ.
The (Lorentz) metric tensor
We use this to measure the length of vectors in regions of space-time so small that we can
represent it by a region in ℝ4. In the Cartesian coordinate representation, the matrix representing
this metric has coordinates h = 
In Cartesian coordinates, h=h-1. Some other coordinate systems are not as forgiving.
We often interpret a vector as a column matrix, and a 1-form as a row matrix.
The inner product of two vectors a, b is denoted by a·b. Various notations include:
- In coordinates: -a0b0+a1b1+a2b2+a3b3, where a0..a3, b0..b3 are the coordinates of a and b
respectively.
- Matrix notation: aThb
- Note: by definition, the metric tensor is symmetric: a·b=b·a . Thus, when both
a and b are represented in the same coordinate system, then the matrix h representing the
metric tensor is also symmetric: h = hT
- A shorthand for a·a is a2. [Clearly, this is not a general power notation: the result is a scalar,
rendering a·a·a meaningless....]
Once we have the metric tensor, we can convert between a vector a and its corresponding 1-form
ã, and back.
Converting from a to ã is called "raising the index of a". We define this as (ha)T=:ã
Converting from ã to a is called "lowering the index of ã".
In spite of the fact that both "raising the index" and "lowering the index" are defined in matrix
mathematics (which requires an explicit coordinate system), both of these operations are
coordinate-free. However, these operations require the metric to exist.
Another alternate notation for a·b is <ã,b>.
ℝ4, with the Lorentz metric, is also known as Minkowski space. We can define the
tangent Minkowski space to the space-time manifold at each point in space-time.
Physical formulae
All of these are exercises (worked or otherwise) in Wheeler's "Gravitation".
- u2 = -1 (regardless of geometric units or not!)
- m2 = E2 - p2
- This is in five parts: let a particle with rest mass m and 4-momentum r be examined by an
observer with 4-velocity u. Then:
- E = -r·u
- m2 = -r2
- |p|2 = (r·u)2+r2
- |v| = |p|/E
- v = [r+(r·u)u]/[-r·u]
- Let T be a function from (a region of) space-time into ℝ. [Wheeler's example is the
temperature inside the Sun.] Consider a cosmic ray that flies through the region with 4-velocity u. [I will suppress the argument of T, here].
- dT/dt = ¶uT = <dT,u>
- In a local Lorentz frame, dT/dt = ua Ta [=...]
Einstein-de Broglie equations
These are derivable from classical electromagnetic theory for photons. However, quantum
mechanics defines these to apply to objects with nonzero rest mass. They relate energy E to
frequency n and conventional momentum p to wavelength l, in a Lorentz frame.
Alternate formulation:
EXERCISE: define w, |k| so that these are the same equations.
NOTE: The definition p=hk provides
a conversion between the relativistic conventional momentum vector p and the quantum
?? vector k.
The first equation, when applied to a photon, is simply Einstein's equation for photon energy.
Lorentz and Poincaré transforms
Lorentz transforms are the space-time analog of rotations in ℝ3. Poincaré transforms are
Lorentz transforms with an origin shift applied afterwards. These are both coordinate-change operations.
Wheeler denotes a Lorentz transform by Lab, where
- a denotes the Lorentz frame being converted from
- b denotes the Lorentz frame being converted to
In matrix notation, the conversion from the 4-vector ua to the 4-vector ub is ub:=Labua .
From the above description:
- The Lorentz transforms Lab and
Lba are inverse coordinate transformations.
- For all Lorentz frames a, the Lorentz transform Laa is
the identity Lorentz transform.
Two example Lorentz transforms:
- Rotation in the x-y plane by angle q:
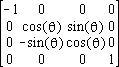
- slope s:=tan(q)
- if two rotations by angles q1, q2
are done consecutively, the resulting rotation is by angle q1+q2. The corresponding
slope is from the angle addition formula for tan(q).
- Boost of reference frame by velocity parameter a in the z-t plane:
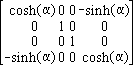
- Speed b:=tanh(a)[=c·tanh(a) in conventional units]
- The velocity parameter for consecutive boosts by a1, a2 is a1+a2. The corresponding
speed is from the "parameter addition" formula for tanh(a).
As long as we're discussing Lorentz transforms, we should also notice the Lorentz contraction factor 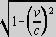 , where v is the norm of the 3-velocity
of the object relative to a Lorentz frame. [This factor has not been geometrized.] We have the following relations involving this factor:
, where v is the norm of the 3-velocity
of the object relative to a Lorentz frame. [This factor has not been geometrized.] We have the following relations involving this factor:
- m=m0/
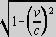 , where m is the mass-energy of the object in the Lorentz frame, and m0 is the rest mass-energy of the object.
, where m is the mass-energy of the object in the Lorentz frame, and m0 is the rest mass-energy of the object.
- L=
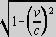 L0, where L is the length of the object, in its direction of travel, in the Lorentz frame, and L0 is the rest length of the object, in its direction of travel relative to the Lorentz frame.
L0, where L is the length of the object, in its direction of travel, in the Lorentz frame, and L0 is the rest length of the object, in its direction of travel relative to the Lorentz frame.
- T=
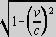 T0, where T is the elapsed time in the Lorentz frame, and T0 is the elapsed time for the object.
T0, where T is the elapsed time in the Lorentz frame, and T0 is the elapsed time for the object.
Gravity via a uniformly accelerating rocket
One of the key principles of General Relativity is that gravity cannot be distinguished from
uniform acceleration. Thus, we can (in principle) study the laws of physics in a practically uniform
gravity field by converting them from an inertial reference frame to a uniformly accelerating reference
frame [say, a passenger in a uniformly accelerating rocket]. The actual emulation is done in a tangent Minkowski space.
Let's take a look at the uniformly accelerating passenger. Since his 4-velocity u is not changing in
magnitude, we know that it is (Lorentz) orthogonal to his 4-acceleration a.
Let's simplify the coordinate system for this. Since the 4-acceleration is uniform, we can Lorentz-transform our coordinates
so that all of the 4-acceleration is in the t-z plane. Then the x and y-coordinates are constant; translate the
coordinate system so that these are zero.
Then the equations we want are:
- 0=u·a=-ut[dut/dt]+uz[duz/dt]
- -1=u·u=-ut2+uz2
These equations should look strangely familiar [cf. Hyperbolic Trigonometry: A Crash Review.]
In particular, for any nonzero real number g:
- 1=cosh2(gt)-sinh2(gt)
- [d/dt]cosh(gt)=g·sinh(gt)
- [d/dt]sinh(gt)=-g·cosh(gt)
It is a routine algebraic exercise to verify that
- ut(t)=cosh(gt)
- uz(t)=sinh(gt)
satisfies the target equations. We then integrate to get
- xt(t)=[1/g]sinh(gt)
- xz(t)=-[1/g]cosh(gt)
We use a coordinate translation to force all four arbitrary constants to 0. It should also be noted
that the choices for ut and uz may be independently negated.
We are now in a position to compute the (non-rotating) Fermi-Walker tetrad for the uniformly accelerated observer, as
a function of t. VERIFY: the following four basis vectors are all orthogonal
and have unit length (under the Lorentz metric). Furthermore, verify that et(t)
is tangent to the trajectory of the uniformly accelerated observer for all real numbers t.
- et(t)=(cosh(gt),0,0,sinh(gt))
- ex(t)=(0,1,0,0)
- ey(t)=(0,0,1,0)
- ez(t)=(sinh(gt),0,0,cosh(gt))
The Fermi-Walker tetrad serves as a local coordinate system, which will eventually turn into garbage &endash; even in flat spacetime.
From the viewpoint of the uniformly accelerating observer, the Fermi-Walker tetrad coordinate system is the one he is measuring
in. However, the coordinate forms of the laws of physics are not those of a Lorentz frame. While for each
t, the coordinate system is a Lorentz frame, the Lorentz frame for the Fermi-Walker tetrad coordinate system is
a function of t.
Free-fall in a uniform gravity field
We are now ready to compute the trajectory (of the center of gravity) of a body in free-fall in a
uniform gravity field. To do this, recall that all Lorentz frames are in free-fall. Thus, if we
convert a trajectory that is a straight (time-like) line in an inertial frame to a uniformly accelerated
local coordinate system (as explained above), we should get the trajectory of a body in free-fall in a
uniform gravity field.
This exercise should also give us some idea of how to relate g (here) to g (in classical physics). We have been
misusing the notation so far.
We consider an object that reaches its maximum height z=K-1/g at t=0.
The trajectory of this object (in the Lorentz frame we chose to define the uniformly accelerated coordinate system relative to)
is simply
- tLorentz unconstrained
- xLorentz=constant
- yLorentz=constant
- zLorentz=1/g
The relevant coordinates are tLorentz, zLorentz, and zgravitized, the latter
being computed for each t from the basis vectors as a function of t, with origin the location
of the uniformly accelerated observer at time t in the Lorentz frame. [tgravitized is simply t for
the uniformly accelerated observer.]
Working in the Lorentz-frame z-t plane, for each t we construct a Euclidean-metric right triangle:
- The legs are parallel to the Lorentz-z and Lorentz-t axes.
- The direction vector is Lorentz-orthogonal to et(t), so
is ±ez(t).
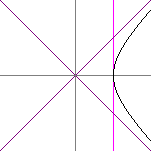 Now, zgravitized is simply the oriented Euclidean length of the hypotenuse of the above triangle. VERIFY:
Now, zgravitized is simply the oriented Euclidean length of the hypotenuse of the above triangle. VERIFY:
- The oriented Euclidean length of the leg of the triangle parallel to the Lorentz-z axis is [1/g][gK-cosh(gt)].
[This is a nonpositive real number.]
- the oriented Euclidean length of the hypotenuse is [1/g][gK-cosh(gt)][1+tanh2(gt)].
Thus, we have computed:
zgravitized(t)=[1/g][gK-cosh(gt)][1+tanh2(gt)]
VERIFY: the power series expansion for the above, when K=1/g, is -gt2/2+o(t4)...
So g (as we have been using it) is g as in classical mechanics [as we have been misusing the notation prior to now]. Since
we are choosing units such that the speed of light c=1, g must be expressed in these units.
- NOTE: The entire hyperbola, that is the path of the uniformly accelerated observer, is within a region
that is related in a space-like way to the origin. So, the Fermi-Walker tetrad local coordinate system that
the uniformly accelerated observer uses must break down in the z-t coordinate plane at a
z-distance of at most 1/g [namely. z=-1/g]. [In a perfectly flat space-time, this is attained: all lesser z-distances are possible.] This also suggests (geometrically) that
all of the free-fall trajectories enter and leave the the Fermi-Walker tetrad local coordinate system at z=-1/g.
- Since the hyperbola (as a curve) is invariant under Lorentz transforms, the Fermi-Walker tetrad local coordinate system breaks down at (or before) z=-1/g for all proper times t. To test
the Fermi-Walker tetrad local coordinate system more thoroughly, we would want to have free-fall trajectories with maximum heights from just above -1/g to ¥. However, this is very similar algebra;
we simply replace 1 by gK in the above derivation. The maximum height is then K-1/g, which is positive when the world-line of the free-fall object passes
through the hyperbola twice, and negative when it does not intersect the hyperbola at all.
- Let's see how long it takes an object in a uniform gravity field to
free-fall from a height of (just above) -1/g to a maximum height of K-1/g and back to a height of (just above) -1/g. First, try to set the height to -1/g and factor out 1/g:
- -1=[gK-cosh(gt)][1+tanh2(gt)]
- i.e. 0=gK+1+tanh2(gt)-cosh(gt)-sinh(gt)tanh(gt)
- i.e. 0=gK+1+sech2(gt)[sinh2(gt)-cosh3(gt)-sinh2(gt)cosh(gt)]
- At t=0, the RHS of the above equation is gK. The RHS is an even function. We want to solve for t, of smallest absolute value, that makes the equation true. The proper time we want is
twice this absolute value of t.
- At this point, those who prefer numerical solutions may take this
equation and play with it numerically, skipping the rest of my algebraically gory discussion.
- Now, the second factor looks like it should be third degree in cosh(gt):
- 0=gK+1+sech2(gt)[[cosh2(gt)-1]-cosh3(gt)-[cosh2(gt)-1]cosh(gt)]
- i.e. 0=gK+1+sech2(gt)[-2cosh3(gt)+cosh2(gt)+cosh(gt)-1]
- i.e. 0=sech2(gt)[-2cosh3(gt)+[gK+2]cosh2(gt)+cosh(gt)-1]
- The above is now susceptible to exact solution for cosh(gt) via the cubic formula. Since sech(gt) is nonzero for all real t, we have:
- 0=2cosh3(gt)-[gK+2]cosh2(gt)-cosh(gt)+1
- i.e. 0=cosh3(gt)-([gK+2]/2)cosh2(gt)-[1/2]cosh(gt)+1/2. At this point, take out a handbook of math tables containing the solution for a cubic equation:
- Write w:=cosh(gt)-[gK+2]/6; then the above becomes
- 0=w3+[1/3][3·[-1/2]-[[gK+2]/2]2]w+[1/27][2[[gK+2]/2]3-9[[gK+2]/2][-1/2]+27[1/2]]
- i.e. 0=w3-[1/12][6+[gK+2]2]w+[1/108][(gK+2)3+9[gK+2]+54]
- Before continuing, let us inspect the sign of the discriminant of this cubic equation:
[[1/108][(gK+2)3+9[gK+2]+54]]2/4+[-[1/12][6+[gK+2]2]]3/27. [I hope this cancels out; otherwise, it's going to be
sixth degree in gK....]
- i.e., the sign of [(gK+2)3+9[gK+2]+54]2/[4·1082]-[6+[gK+2]2]3/[27·123] [moving all of the constant multipliers out of the powers]
- i.e., the sign of [(gK+2)3+9[gK+2]+54]2-[6+[gK+2]2]3 [removing a factor of 1/64, then a factor of 1/729. These factors go back in when we do the discriminant.]
- It's time to expand things in powers of gK:
- i.e., the sign of [(gK)3+6(gK)2+12gK+8+9gK+18+54]2-[6+(gK)2+4gK+4]3
- i.e., the sign of [(gK)3+6(gK)2+21gK+80]2-[(gK)2+4gK+10]3
- At this point, it should be clear that the above expression, after reduction, will only be at most fourth degree in gK.
- i.e., the sign of [42+36-30-48](gK)4+[160+252-240-64](gK)3+[960+441-300-480](gK)2+[3360-120]gK+[802-103]
- i.e., the sign of 108(gK)3+621(gK)2+3240gK+5400 -- which is always positive, since K is positive. Thus, there is one real root of the above equation [in w]. There is a factor of 27 in the above, so the actual discriminant is
- [4(gK)3+23(gK)2+120gK+200]/[64·27]
- The real root of the cubic equation (in w) is then
- (-([1/108][(gK+2)3+9[gK+2]+54])/2+[4(gK)3+23(gK)2+120gK+200]/[64·27])1/3+
(([1/108][(gK+2)3+9[gK+2]+54])/2+[4(gK)3+23(gK)2+120gK+200]/[64·27])1/3
- =(-[(gK+2)3+9[gK+2]+54]/216+[4(gK)3+23(gK)2+120gK+200]/[64·27])1/3+
([(gK+2)3+9[gK+2]+54]/216+[4(gK)3+23(gK)2+120gK+200]/[64·27])1/3
- =[1/12][(-8[(gK+2)3+9[gK+2]+54]+[4(gK)3+23(gK)2+120gK+200])1/3+
(8[(gK+2)3+9[gK+2]+54]+[4(gK)3+23(gK)2+120gK+200])1/3]
- =[1/12][(-8[(gK)3+6(gK)2+12gK+8+9gK+18+54]+[4(gK)3+23(gK)2+120gK+200])1/3+
(8[(gK)3+6(gK)2+12gK+8+9gK+18+54]+[4(gK)3+23(gK)2+120gK+200])1/3]
- =[1/12][(-[8(gK)3+48(gK)2+168gK+640]+[4(gK)3+23(gK)2+120gK+200])1/3+
([8(gK)3+48(gK)2+168gK+640]+[4(gK)3+23(gK)2+120gK+200])1/3]
- =[1/12][(-4(gK)3-25(gK)2-48gK-440)1/3+
(12(gK)3+71(gK)2+288gK+840)1/3]
- VERIFY: This root is a positive real number. However, to yield a solution for cosh(gt), we need this root to be
at least 1-[gK+2]/6. In this case, |t| = [1/g][cosh-1([root]+[gK+2]/6)] when the freely-falling object enters or leaves
the Fermi-Walker tetrad local coordinate system
Normalization of quantum state functions
This is the mathematical way of stating that a quantum-mechanical system has to be somewhere.
After studying my text and considering how to extrapolate the text, I'm going to state the
normalization condition for a particle this way:
At all points x in space-time, the state function Y : (space-time) ® ℂ of a particle, when extrapolated to the tangent Minkowski space for the point x,
satisfies
ó
ôY(x,t)*Y(x,t) dx = K positive in ℝ.
õℝ3
for all Lorentz frames of the tangent Minkowski space (i.e. x in space-time).
K is the normalization factor for Y(x,t) in the Lorentz frame it is computed for, at that point (x,t) in space-time. For the tangent Minkowski space, K is constant for all times t in the given Lorentz frame.
To normalize Y(x,t) for the Lorentz frame in the tangent Minkowski space, divide Y(x,t) by the positive square root of K; this
makes the transformed integral = 1. [This may be viewed as a pointwise normalization, for a specific Lorentz frame, of the state function in space-time.]
NOTE: |Y(x,t)|2 = Y(x,t)*Y(x,t), where * denotes
conjugation of complex numbers.
Now, referring back to the uniformly accelerated observer: what he can observe of his constant-time
space slices "burns out" before z=-1/g. However, the normalization condition for quantum state functions (which refers to these space-slices
in the Lorentz frame his constant-time space slices extend to) ignores this restriction.
Also, note that any complex number with absolute value 1 may be factored globally out of the state function Y without
affecting the normalization integral for any tangent Minkowski space. This symmetry is demanded of all quantum operators for observable quantities.
We thus consider a quantum state function Y to be equivalent to eidY,
for any d in ℝ.
Electromagnetism in a tangent Minkowski space
First, some more terminology. In a fixed Lorentz frame, we denote:
- The electric field (as measured in ℝ3) as E=(Ex,Ey,Ez).
- The magnetic field (as measured in ℝ3) as B=(Bx,By,Bz).
- The Faraday 2-form as
F =
| Exdx^dt |
+Bxdy^dz |
| +Eydy^dt |
+Bydz^dx |
| +Ezdz^dt |
+Bzdx^dy |
. This is a coordinate rearrangement: the coordinates of B and E are used as-is in the Faraday 2-form.
- Since we have a differential-geometric metric (the Lorentz metric), we can use the standard definition of Hodge duality to define
the Maxwell 2-form as Hodge-dual to the Faraday 2-form. That is: the Maxwell 2-form is defined by
*F :=
| -Bxdx^dt |
+Exdy^dz |
| -Bydy^dt |
+Eydz^dx |
| -Bzdz^dt |
+Ezdx^dy |
.
Clearly, our first task is to recover the usual laws of electromagnetism from the above. We will expect some corrections to
be necessary in the presence of gravity, but presume that Earth's miniscule g should not induce gross corrections (third
significant digit or larger).
We consider a particle with a 4-velocity vector u (implicitly a function of that particle's proper time t). We give it an
electric charge e. We then directly generalize Newton's definition of force to momentum 1-forms and velocity 4-vectors:
dr/dt := eFu
Now, let's convert this to matrix notation:
| [drt/dt drx/dt dry/dt drz/dt] := e |
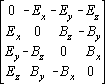 |
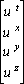 |
This, after evaluation of the right hand side as a matrix product, yields:
drt/dt dt = e(-Exux-Eyuy-Ezuz) dt
drx/dt dx = e(Exut+Bzuy-Byuz) dx
dry/dt dy = e(Eyut+Bxuz-Bzux) dy
drz/dt dz = e(Ezut+Byux-Bxuy) dz
Next, let us consider the magnetostaticdynamic law
dF=0
for a Minkowski tangent space:
d( Exdx^dt + Bxdy^dz
+Eydy^dt + Bydz^dx
+Ezdz^dt + Bzdx^dy) = 0 (3-form over ℝ4)
Skip the math?
Now, to evaluate this: technically, each E_ and B_ is going to have a partial
derivative term, matched with a corresponding d_ term. A priori: each basis 2-form, when differentiated over ℝ4,
should yield four 3-form terms in its derivative. This would have us combine, a priori, 24 3-form terms.
However, terms like dx^dx are automatically 0. This is a general fact about 1-forms when they
are combined by a wedge product into an k-form. Thus, we only have twelve 3-forms to algebraically combine.
EXERCISE: When the factors of the wedge product are written in canonical order, the
number of basis k-forms over ℝn is the combinatoric function "n choose k".
So, the first stage of the calculation yields:
d( Exdx^dt + Bxdy^dz
+Eydy^dt + Bydz^dx
+Ezdz^dt + Bzdx^dy) =
¶Ex/¶y dx^dt^dy
+¶Ex/¶z dx^dt^dz
+¶Bx/¶t dy^dz^dt
+¶Bx/¶x dy^dz^dx
+¶Ey/¶x dy^dt^dx
+¶Ey/¶z dy^dt^dz
+¶By/¶t dz^dx^dt
+¶By/¶y dz^dx^dy
+¶Ez/¶x dz^dt^dx
+¶Ez/¶y dz^dt^dy
+¶Bz/¶t dx^dy^dt
+¶Bz/¶z dx^dy^dz
Now, let's put these terms into standard form, and collect the coefficients before setting
them equal to zero. Remember that the wedge product is anti-commutative: dx^dy=-dy^dx, for
instance. We get:
(-¶Ex/¶y + ¶Ey/¶x + ¶Bz/¶t) dt^dx^dy = 0 dt^dx^dy
(-¶Ex/¶z + ¶Ez/¶x - ¶By/¶t) dt^dx^dz = 0 dt^dx^dz
(-¶Ey/¶z + ¶Ez/¶y + ¶Bx/¶t) dt^dy^dz = 0 dt^dy^dz
(¶Bx/¶x + ¶By/¶y + ¶Bz/¶z) dx^dy^dz = 0 dx^dy^dz
After removing the units (3-forms over ℝ4) and negating both sides
of the dt^dx^dz equation, we get:
(-¶Ex/¶y + ¶Ey/¶x + ¶Bz/¶t) = 0
(-¶Ez/¶x + ¶Ex/¶z + ¶By/¶t) = 0
(-¶Ey/¶z + ¶Ez/¶y + ¶Bx/¶t) = 0
(¶Bx/¶x + ¶By/¶y + ¶Bz/¶z) = 0
The above should be familiar to those with a physics background: the first three equations is the component form of
the classical magnetodynamic equation, and the last equation is the classical magnetostatic equation.
Now, let us consider the electrostaticdynamic law
d*F=4p*J
for a Minkowski tangent space.
Skip the math?
I already mentioned what the Maxwell 2-form *F was. So,
when we take its derivative:
d( -Bxdx^dt + Exdy^dz
-Bydy^dt + Eydz^dx
-Bzdz^dt + Ezdx^dy) =
¶-Bx/¶y dx^dt^dy
+¶-Bx/¶z dx^dt^dz
+¶Ex/¶t dy^dz^dt
+¶Ex/¶x dy^dz^dx
+¶-By/¶x dy^dt^dx
+¶-By/¶z dy^dt^dz
+¶Ey/¶t dz^dx^dt
+¶Ey/¶y dz^dx^dy
+¶-Bz/¶x dz^dt^dx
+¶-Bz/¶y dz^dt^dy
+¶Ez/¶t dx^dy^dt
+¶Ez/¶z dx^dy^dz
Now, let's put these terms into standard form, and collect the coefficients. Again,
recall that the wedge product is anti-commutative: dx^dz=-dz^dx, for instance. We get:
(¶Bx/¶y - ¶By/¶x + ¶Ez/¶t) dt^dx^dy
(¶Bx/¶z - ¶Bz/¶x - ¶Ey/¶t) dt^dx^dz
(¶By/¶z - ¶Bz/¶y + ¶Ex/¶t) dt^dy^dz
(¶Ex/¶x + ¶Ey/¶y + ¶Ez/¶z) dx^dy^dz
We need to set the above to *J -- but how to interpret it?
First, *J is the Hodge dual of the 1-form dual to the charge-current density vector
(r,jx,jy,jz)
under the Lorentz metric. This 1-form is:
-r dt + jx dx + jy dy + jz dz
EXERCISE: verify the above calculation using the matrix notation for computing the 1-form dual
to a vector.
The first stage of computing the Hodge dual yields the following 3-form:
r dx^dy^dz - jx dt^dy^dz + jy dt^dx^dz - jz dt^dx^dy
The calculation runs as follows:
- List the 1-form d_, and then the 3-form wedge product (in canonical order) that must be wedged to this to get a 4-form:
dt^dx^dy^dz
dx^dt^dy^dz
dy^dt^dx^dz
dz^dt^dx^dy
- The required sign coefficients in the Hodge-dual 3-form is -1 for an even permutation, and
1 for an odd permutation. This is because we are taking the Hodge dual of forms rather than
tensors, and the Lorentz metric has an odd number of -1 entries on its diagonal.
dt^dx^dy^dz: dx^dy^dz term has vector coefficient negated
dx^dt^dy^dz: dt^dy^dz has vector coefficient unchanged
dy^dt^dx^dz: dt^dx^dz has vector coefficient negated
dz^dt^dx^dy: dt^dx^dy has vector coefficient unchanged
We now set the two sides equal to each other:
(¶Bx/¶y - ¶By/¶x + ¶Ez/¶t) dt^dx^dy = -jz dt^dx^dy
(¶Bx/¶z - ¶Bz/¶x - ¶Ey/¶t) dt^dx^dz = jy dt^dx^dz
(¶By/¶z - ¶Bz/¶y + ¶Ex/¶t) dt^dy^dz = -jx dt^dy^dz
(¶Ex/¶x + ¶Ey/¶y + ¶Ez/¶z) dx^dy^dz = r dx^dy^dz
After removing the units (3-forms), and negating both sides of the dt^dx^dz equation, we get the following
equations:
(¶Bx/¶y - ¶By/¶x + ¶Ez/¶t) = -jz
(¶Bz/¶x - ¶Bx/¶z + ¶Ey/¶t) = -jy
(¶By/¶z - ¶Bz/¶y + ¶Ex/¶t) = -jx
(¶Ex/¶x + ¶Ey/¶y + ¶Ez/¶z) = r
The above should be familiar to those with a physics background: the first three equations is the component form of
the classical electrodynamic equation, and the last equation is the classical electrostatic equation.
TODO: A-field; etc.
TODO: digressions: Hodge duality, wave operator
AMAZON.COM® is the registered trademark of Amazon.com, Inc.
Opinions, comments, criticism, etc.? Let me know about it.
Return to the GR+QM page, the Math page, or the main page.
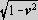
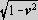 , j=1..3
, j=1..3
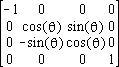
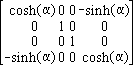
 Now, zgravitized is simply the oriented Euclidean length of the hypotenuse of the above triangle. VERIFY:
Now, zgravitized is simply the oriented Euclidean length of the hypotenuse of the above triangle. VERIFY: