Signs in the Heavens
I'm looking for [conjunctions, sextiles, trines, squares,
quintiles] of [Sun, Moon, Mercury, Venus, Mars, Jupiter, Saturn,
Uranus, Neptune, Pluto, North Node, South Node, Trans-plutonian,
...]
Visit  Rollan
McCleary. I am more interested in signs for those attuned to
Astronomy, other Western sciences, or Eschatology.
Rollan
McCleary. I am more interested in signs for those attuned to
Astronomy, other Western sciences, or Eschatology.
- Before 1800, Astronomy and Astrology are one discipline.
Books of interest
What are you surveying here?
My fantasy is to track 'anomalies' in the First and Second Heavens.
Understanding what is usual for the First and Second Heavens is
required in order to notice what an 'anomaly' is....
- The First Heaven conventionally
covers the Earth's atmosphere. I will also include the Earth's
magnetosphere in this category, and related phenomena.
- The Second Heaven conventionally
includes everything beyond the Earth's atmosphere. I will define
this to be the vacuum of space, and anything normally separated
from Earth by the vacuum of space.
- The Third Heaven is not accessible to even Science At The
Limit. I quote the Apostle Paul:
It is doubtless not profitable for me to boast. I will
come to visions and revelations of the Lord: I know a man in Christ
who fourteen years ago -- whether in the body I do not know, or
whether out of the body I do not know, God knows -- such a one was
caught up to the third heaven. And I know such a man -- whether in
the body or out of the body, I do not know, God knows -- how he was
caught up into Paradise and heard inexpressible words, which it is
not lawful for a man to utter. Of such a one I will boast; yet of
myself will I not boast, except in my infirmities. For though I
might desire to boast, I will not be a fool; for I will speak the
truth. But I refrain; lest anyone should think of me above what he
sees me to be or hears from me.
[II Cor. 12:1..6, NKJV]
General resources
Nick
Strobel's Introductory astronomy notes
National
Geographic Star Chart
Satellite-track star charts
Chris Dolan's Interactive Star Chart. [No Java, no star
charts!]
Encyclopedia of Standard Planetary Information, Formulas and
Constants
International Astronomical Union
 Near Earth
Object Program
Near Earth
Object Program
International Meteor
Organization, and a mirror
American Meteor Society
 U.S. NASA multimedia
gallery
U.S. NASA multimedia
gallery
 Index to
U.S. NASA projects
Index to
U.S. NASA projects
Mullard Space Science Laboratory (U.K.)
MIT Center for Space Research Project Index
GRACE -- Gravity Recovery and Climate Experiment
EXERCISE: try to figure out when I'm paraphrasing the resources
I mention above -- and which one.
Most other exercises, below, are explicitly worked in one of the
above general resources.
Weather-related links:
Weather Processor Take a
look at the meteorologists' forecasting charts.
Drudge Weather
Report® Several useful summaries -- but watch out when
going to the home page....
 National
Hurricane Center Updates every 3-6 hours when there is a
tropical storm or hurricane. Several hurricanes in 1998 easily
overtaxed its Web hardware.
National
Hurricane Center Updates every 3-6 hours when there is a
tropical storm or hurricane. Several hurricanes in 1998 easily
overtaxed its Web hardware.
Atlantic Tropical Weather Center
Prepare to be swamped. When I was using this in 1998, it had 6
pages of technical reports. I was unable to understand most of
these. This provides an index of mirrors to the National Hurricane
Center links fairly early.
Interpreting the temperature is a survival skill even when
infrastructure [electric grid, water utilities, etc.] is
functioning at Western standards.
Heat index charts
- UNISYS
Temperature is in F°. Either dewpoint or relative humidity can
be used as the second parameter.
Wind chill charts
- UNISYS
Temperature is in F°. Wind speed is in knots (nautical miles
per hour).
The Earth's atmosphere
The French meteorologist Léon-Philippe Teisserenc de Bort
conjectured, in 1902, that the Earth's atmosphere could be
meaningfully described in vertically layered segments. He decided
to call the lowest layer (the layer in which all conventional
weather occurs) the troposphere (Greek roots: "sphere of change"),
and the layer(s) above it the stratosphere (Greek roots: "sphere of
layers"). He called the division between these layers the
tropopause. His measurements (sending unmanned balloons up with
barometers, thermometers, etc.) indicated that over France, the
tropopause was about 7 miles up.
The height of the tropopause varies from about 10 miles at the
equator to about 5 miles at the poles, and is about 7 miles high in
the mid-latitudes (circa 45° north or south). These heights
are measured from sea level.
The stratosphere (the layer Léon-Philippe Teisserenc de
Bort's balloons reached) extends to about 30 miles above sea level.
Temperatures generally range from -40°F to -100°F. Except
for the lower reaches of the jet stream, the stratosphere is
virtually windless.
It should be noted that ozone (O3) has measurable
concentrations from about 6 miles above sea level to the top of the
stratosphere. Most ozone formation happens 20-30 km above sea
level, as a side-effect of absorption of UV radiation (particularly
UV-C) by oxygen (O2); the temperature in this layer
climbs from -60°F to 130°F in less than 200 feet.
The mesosphere extends from the end of the stratosphere to about
50 miles above sea level. Temperatures generally decrease with
height, attaining a low of -225°F in the summer. The
mesosphere is warmer in the winter than in the summer. This is
conjectured to be due to a heat-exchange effect. Most meteors burn
up in the mesosphere. The upper range of the jet stream is in the
lower mesosphere.
I would naïvely conjecture that increasing the "thermal
inertia" of the atmosphere by augmenting carbon dioxide
(CO2) should reduce the temperature in the mesosphere,
since summer already reduces the temperature of the mesophere
compared to winter. At least one U.S. NASA simulation (I'd have to
search archives, but it was clipped to MyCNN during the year 1999
or 2000) has confirmed this at an altitude of 40 miles above sea
level.
Note: the popular literature calls 'increasing the
"thermal inertia" of the atmosphere by augmenting carbon dioxide'
the "greenhouse effect". This is not a simple heating up; rather,
all weather systems have their thermal energy increased,
permitting increased severity.
The jet stream(s) are a thin (typically 1-2 miles high), wide
(typically 180-300 miles wide) band of wind (ranging from 60 miles
per hour to an extreme of about 290 miles per hour, but usually not
faster than 150 miles per hour).
The thermosphere extends from the top of the mesosphere, to
about 180 miles above sea level. Temperatures in this region can
fluctuate from highs of about 3,600°F to lows of about
2,600°F.
The exosphere extends from the top of the mesosphere into the
vacuum of space. The latter boundary is very dubious, but may be
safely said to be somewhere between 300 and 900 miles above sea
level. The main components here are hydrogen, helium, and oxygen
(often monoatomic). Some of these atoms attain escape velocity and
leave the Earth indefinitely.
The above was abstracted from, among other sources, "It's
Raining Frogs and Fishes: Four Seasons of Natural Phenomena and
Oddities of the Sky" by Jerry Dennis, published by
Harper-Collins.
The Earth's magnetosphere
 Space
Weather U.S. NASA's space weather information.
Space
Weather U.S. NASA's space weather information.
This section is not implemented yet.
Naked Eye Astronomy
An online planetarium.
The 'celestial sphere' is a useful perceptual artifact. It results
from the following:
- Human vision cannot effectively use parallax information to
judge distance beyond 'optical infinity' (about 500 feet). [That
is, for those 97-98%(?) of the people who have true stereoscopic
vision.]
- At the distance scales normally used in astronomy (certainly
the moon and beyond), precision measurements are required to detect
parallax at all. For instance, using a specific diameter of the
Earth's orbit as a baseline, Proxima Centauri's apparent position
is shifted by about 1.54 arc-seconds when viewed from opposite
endpoints of this diameter. This yields a reported parallax of 0.77
arc-seconds. (Proxima Centauri is 11th magnitude. The nearest
visible star is Alpha Centauri -- 4.4 light-years away,
rather than Proxima Centauri's distance of 4.2 light-years).
This means that Earth-based observations need only specify two
out of the three 3-d spherical coordinates: the angle theta
(angular offset from the celestial zero north-south meridian), and
the angle phi (angular offset from the celestial equator). The
radius r cannot be measured directly. Alternatively, we could use
offsets from the observer's meridian and horizon (defined
before).
EXERCISE: Since the sun and stars rise in the east and set in
the west, which way does the Earth rotate?
There is at least one low-tech way to know that the Earth is
spherical without extensive travel: lunar eclipses. Pythagoras
(ancient Greece) noted that in a lunar eclipse, the shadow of the
Earth on the Moon is always curved, and always has the same degree
of curvature. The only type of object whose shadow has this
property, regardless of orientation, is a sphere. [In practice,
this means that within the observational error above, the Earth is
a sphere. This means that the difference in the polar diameter,
versus equatorial diameter(s), of the Earth does not affect the
visible curvature of the shadow of the Earth. There should
be a slight difference because a certain amount of gravitational
acceleration+tension forces at the equator is required to anchor
the Earth's crust to the Earth. This difference is measurable.]
Eratosthenes (approximately 276BC-195BC) took advantage of his
position as the Librarian at the great Museum in Alexandria to
estimate the circumference of the Earth from this. He noted that at
summer solstice, there was no visible shadow at noon in Alexandria
(use a deep well to check this), but there was a shadow at
Syene at summer solstice. The angle of this shadow was just over
7°. From this, he estimated that the distance between
Alexandria and Syene was 1/50th of a great circle. Since the
distance between the two cities was "5,000 stadia", the
circumference of the Earth was "250,000 stadia". Unfortunately, we
don't have a clear idea what his length unit was in our units.
Conventional approximations suggest his figure was about 47,000
kilometers/29,000 miles (two significant digits), versus a modern
five-significant-digit approximation of 40,074 kilometers/24,902
miles. [Abbreviated forms of these: "47,000 km/29,000 mi (two
significant digits), versus a modern five-significant-digit
approximation of 40,074 km/24,902 mi". Yes, the period is
deliberately not used in the abbreviation for miles, contravening
the usual grammatical rule for abbreviations that use direct
truncations.]
You might try clicking on the left or right third of the
celestial sphere illustration, below--to rotate it.
The north and south celestial poles [following Strobel, I
will use the acronyms NCP and SCP respectively when I don't need
literary parallelism] are defined by the Earth's rotation axis.
That is:
- The Earth's rotation axis intersects the celestial sphere,
directly over the north pole, at the north celestial pole. It is
visible in the northern hemisphere, and on the horizon on the
equator.
- The Earth's rotation axis also intersects the celestial sphere,
directly over the south pole, at the south celestial pole. It is
visible in the southern hemisphere, and on the horizon at the
equator.
The celestial equator is the 'great circle' in the celestial sphere
that is equidistant from both the north and south celestial poles.
Except at the North and South poles, the celestial equator
intersects the horizon at due east and due west.
- At the North and South Poles, due east and due west are
meaningless, so we know the above description breaks down. The
celestial equator is the horizon at the North and South
Poles.
The apparent path of all stars in the sky is parallel to the
celestial equator.
EXERCISE: Explain why the above is true, in terms of the Earth's
rotation and the way we are using spherical coordinates to describe
the celestial sphere. [This may be interpreted as either a math or
an essay question, depending on one's talents. Do it the easy way
for you.]
EXERCISE: What is the angle of the stars' path in the sky
relative to the horizon? [Yes, this depends on your latitude.
HINTS: Interpret 'parallel to the horizon' as an angle of 0°;
this will happen at the North and South Poles. Also, the celestial
north and south poles are on the horizon on the Earth's
equator.]
We are now ready to define celestial coordinate systems. There
are two commonly used: altitude-azimuth, and equatorial. The first
is defined in terms of one's observational point, while the second
is (almost) fixed relative to the stars.
Altitude-azimuth system:
- Altitude: angle above the horizon. [A "negative" angle is
below the horizon, thus not visible.]
- Azimuth: clockwise angle from geographic north.
- Geographic north is not magnetic north, just very close
(most places on Earth, anyway). In the northern hemisphere, Polaris
is the (current) North Star, and will be at practically exactly the
celestial north pole in the year 2007.
Equatorial:
- Right ascension: the time it takes to rotate the object's
position to the local meridian, measured from when the vernal
equinox is at the local meridian. This is measured in hours,
minutes, and seconds; 24 hours = 360°, and the other two
definitions are usual [60 minutes=1 hour, 60 seconds=1 minute].
EXERCISE: work the coordinate conversion table.
- Declination: the angle the object's position makes with the
celestial equator. The North celestial hemisphere has positive
angles, the south celestial hemisphere has negative angles.
[Skip the math!]
Comparison chart:
| spherical coordinates |
geographic |
altitude/azimuth |
equatorial |
| theta |
longitude |
azimuth |
right ascension |
| phi |
latitude |
altitude |
declination |
| orientation with respect to mathematical theta,
phi respectively |
positive, negative [USGS indicates that West
longitudes should be negative] |
negative, negative |
negative, negative |
| net orientation |
negative |
positive |
positive |
I am defining spherical coordinates as radius r, theta
0°-360° counterclockwise, and phi 0° to 180°
from 'vertical up' [analog north pole, zenith] to 'vertical down'
[analog south pole, nadir].
- I know that another common way of defining phi is 90° to
-90° from 'vertical up' to 'vertical down'; however, this can
do strange things to volume and area calculations. [A naive setup
can give negative volumes and/or areas that must be corrected with
absolute values.]
-
[Skip the math!] THIS COMMENT ASSUMES
FAMILIARITY WITH ITERATED INTEGRALS. Things work out correctly for
the volume integral of a sphere, however. We work all the integrals
in radians. For instance, under my preferred definition:
- volume of sphere of radius r = ±

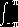
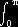 r
2sin(f)
df dq dr
r
2sin(f)
df dq dr
- = ±2p
 r
2
r
2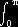 sin(f) df dr
sin(f) df dr
- = ±2p
 r
2 [-cos(f)
r
2 [-cos(f) 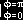 ] dr
] dr
- = ±2p
 r
2 [-cos(p)+cos(0)] dr
r
2 [-cos(p)+cos(0)] dr
- = ±2p
 r
2 2 dr
r
2 2 dr
- = 4p
 r
2 dr
r
2 dr
- With the other common definition, we get:
- volume of sphere of radius r = ±

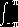
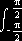 r
2cos(f)
df dq dr
r
2cos(f)
df dq dr
- = ±2p
 r
2
r
2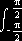 cos(f) df dr
cos(f) df dr
- = ±2p
 r
2 [sin(f)
r
2 [sin(f) 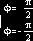 ] dr
] dr
- = ±2p
 r
2 2sin(p/2)
dr
r
2 2sin(p/2)
dr
- = ±2p
 r
2 2 dr
r
2 2 dr
- = 4p
 r
2 dr
r
2 dr
- At this point:
- volume of sphere of radius r = 4p[r
3/3
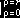 ]
]
- = (4p/3) r
3
Note that the Earth's rotation
[like any other planet's] means that its rotation axis behaves
(roughly) as if it is a gyroscope. Empirically, the precession
period of the Earth-as-gyroscope is about 26,000 years. A list of
candidate pole stars would include Polaris (current), Thuban [in
Draco, ~2000 BCE/BC], Kochab [~1 CE/AD], Deneb [~10,000 CE/AD], and
Vega [~14,000 CE/AD].
- NOTE: The First Coming of Christ was with a well-defined Pole
Star [Kochab].
The effects of the Earth's precession is complicated (and not worth
working in this page). The equinoxes shift by about
360/260°=18/13°=1°23' per century. [Assuming two
significant digits in the precession period, the actual estimate is
somewhere between 1°21' and 1°25' per century.] Since
this is done by shifting the celestial equator (which automatically
shifts the celestial poles!), both declination and right ascension
are affected.
Mr. Strobel has a very elegant explanation of which stars are
above the horizon longer, or shorter, than 12 hours per day.
Circumpolar stars are those stars that either never rise above
the horizon, or never set below the horizon.
- On the equator, the only possible places for circumpolar stars
are the north and south celestial poles.
- In the northern hemisphere, stars with a celestial latitude at
least as far north as 90°-observers latitude are circumpolar,
and always visible. Stars with a celestial latitude as least as far
south as 90°-observer's latitude are circumpolar, and never
visible. [In the southern hemisphere, reverse the visibility
classifications: "north of..." is never visible, and "south of..."
is always visible.].
EXERCISE: Explain why the above statements are correct.
Observational terms that have nothing to do with the 'fixed
stars' (and thus will move relative to the fixed stars as the Earth
rotates):
- Zenith: the point directly overhead. It is 90° above the horizon.
- Nadir: the point directly underneath. It is 90° below the horizon.
- Meridian: the arc through the north point on the horizon, and the south point on the horizon, through the zenith.
[TODO: PICTURE: Zenith, Nadir, meridian, horizon]
EXERCISE: What altitude does the north celestial pole have in
the northern hemisphere? [Alternatively, south celestial pole in
the southern hemisphere; however, the answer will be the same.
Again, this depends on your latitude.]
The solar day, at a given location, may be defined by the time
between consecutive instances of the Sun being on the local
meridian.
NOTE: the Earth's axis is tilted, relative to the Earth's
orbital plane, by about 23.5°. I will omit the word 'about' in
further usage, but it should be kept in mind.
And now, some terms that have to do with the Earth's geography:
- The Tropic of Cancer: the latitude circle of 23.5° N [the
Earth's axis tilt N]. This is defined by the maximum northward
celestial latitude the Sun attains during the year (on the summer
solstice for the Northern hemisphere, winter solstice for the
Southern hemisphere).
- The Tropic of Capricorn: the latitude circle of 23.5° S
[the Earth's axis tilt S] This is defined by the maximum northward
celestial latitude the Sun attains during the year (on the winter
solstice for the Northern hemisphere, summer solstice for the
Southern hemisphere).
- The Arctic Circle: the latitude circle of 66.5° N [90° - the Earth's axis tilt N]
- The Antarctic Circle: the latitude circle of 66.5° S [90° - the Earth's axis tilt S]
[TODO: PICTURE: Equator, all of the above terms]
Areas north of the Arctic circle, or south of the Antarctic
circle, have some calendar days where the sun is above the horizon
24 hours per day. This has prompted the term "land of the midnight
sun".
Now, the Sun appears to drift eastwards relative, relative to
the stars, over a year's time. The path of its drift is the
projection of the Earth's orbit onto the sky; we call it the
ecliptic. Since the Earth's axis is tilted by 23.5° relative
to the Earth's orbital plane, the ecliptic is tilted by 23.5°
relative to the celestial equator.
The ecliptic intersects the celestial equator at two points: the
vernal (spring) and autumnal (fall) equinoxes. [Yes, this is named
for northern hemisphere seasons, for historical reasons.]
- The sun crosses from the south celestial hemisphere to the
north celestial hemisphere at the vernal equinox. This is about
March 21 in the Gregorian calendar.
- The sun crosses from the north celestial hemisphere to the
south celestial hemisphere at the autumnal equinox. This is about
September 22 in the Gregorian calendar.
- For most of the Earth, day and night are both 12 hours long
when the sun is at the equinoxes. Areas with a latitude more
extreme than 89.75° are the exception:
- On the vernal equinox, the sun is rising (very slowly) near the
north pole, and setting (very slowly) near the south pole.
- On the autumnal equinox, the sun is setting (very slowly) near
the north pole, and rising (very slowly) near the south pole.
EXERCISE: Explain why the above exception is correct. This depends
on the angular diameter of the sun, which is about 30' i.e.
0.5°.
North of the Arctic Circle, or south of the Antarctic Circle, if
the Sun's celestial latitude is within 0.25° of 90°-the
observer's latitude, then the Sun is either rising (or setting) the
entire 24 hours of the calendar day.
Most of the above is covered by Mr. Stroebel's notes.
This solar system
Planetary orbits
For a discussion of the near-Newtonian gravity required for
planetary orbits, please see Mr. Strobel's notes.
Tycho Brahe (1546-1601 AD/CE) started a multi-year program to
acquire accurate observational data on planetary positions to test
the Ptolemaic description of apparent planetary motions in the sky.
This started with the construction of an observatory capable of
measurements accurate to one arc-minute (as opposed to ten
arc-minutes anywhere else in Europe) at the Danish island of Hven
in 1576.
Note: Using the Earth's rotation as a baseline, Tycho
Brahe could triangulate out to at least cot(1.5')·cos(latitude
of Hven)·(Earth's radius). Other European observatories were
limited to cot(15')·cos(latitude of observatory)·(Earth's
radius). Numerically, (bounding the cosine below by 0.6), this
works out to a Tychonic triangulation range of at least 2750 Earth
diameters, as opposed to a general European triangulation range of
at least 275 Earth diameters. Similar scaling factors are
applicable to using the Earth's orbit as a baseline. (This is
inconceivable at the time: Copernicus will use Kepler's work to
reconsider a heliocentric solar system, seriously proposed by the
Greek Aristarchus by 280 BC.) The European range is quite enough to
triangulate the distance of the moon. [Hipparchus, a Greek
astronomer based at the island of Rhodes, estimated the distance of
the Moon, from the Earth, as 67.5 Earth radii simply by combining
the apparent speed of the Moon across the sky with the fact that
the Moon exactly covers the Sun during a total solar eclipse. It is
possible to do much better than this.]
Tycho Brahe attempted to measure the change in angular position
of a supernova (as we now call it) that appeared in the
constellation Cassiopeia on November 11, 1572. No change was
measurable, showing that the supernova was almost certainly both
not moving signficantly, and beyond Tycho Brahe's triangulation
range. [Since a common belief (due to Aristotle, a very unempirical
Greek popular with the Roman Catholic Church then) at the time was
that supernovae ["new stars"] were atmospheric phenomena because
they changed, this failure to measure was academically
significant.] Two bright comets in 1577 and 1588 both were measured
as beyond the Moon (causing similar academic difficulties, for the
same reason).
Johannes Kepler (1571-1630 CE/AD) was hired onto Tycho Brahe's
staff in 1600 with the explicit job of retrofitting the Ptolemaic
model to 20 years of observatory data on the apparent position of
the planet Mars. However, Kepler was unable to do so -- the best
fit he found had errors of eight arc-seconds, thus invalidated by
the one arc-second accuracy of Tycho's observatory at Hven. He
empirically constructed the three laws named after him:
- [1609: Astronomia Nova i.e. Commentaries on the
Motions of Mars]
Kepler's First Law: Planetary orbits are ellipses, with the Sun at
one focus.
- [1609: Astronomia Nova i.e. Commentaries on the
Motions of Mars]
Kepler's Second Law: A line drawn between a planet, and the Sun,
sweeps out equal areas in equal times.
- [1619: The Harmony of the World]
Kepler's Third Law:
- (Planet #1's sidereal period/Planet #2's sidereal
period)2
- =(Planet #1's average distance from sun/Planet #2's average
distance from Sun)3
- [NOTE: above is as published. I need to check whether the
correct version depends on semimajor axis (average of perihelion
[minimum] and aphelion [maximum] distances from the Sun).]
Much of the above is from "The Illustrated Encyclopedia of the
Universe", ©2001 The Foundry Media Company Ltd. The exact
publication dates and methods for Kepler's laws is from
"Mathematical Thought from Ancient to Modern Times", ©1972 by
Morris Kline.
The Sun
 SOHO -- Solar and Heliospheric Observatory
SOHO -- Solar and Heliospheric Observatory
- Apparent angular diameter: about 30'
Aristarchus (circa 310 BC/BCE to 230 BC/BCE; based in Alexandria)
attempted the first recorded calculation of the distance from the
Earth to the Sun, in terms of the distance from the Earth to the
Moon. He did this by noting that when the Moon is at first or third
quarter, the Moon is at the right angle of a right triangle formed
by the Earth, Moon, and Sun. Unfortunately, he did not have
accurate measuring technology, and was restricted to using the
chord tables available at the time. Thus, he used a value of
87°, rather than the correct (to within 1 minute) range of
89°50' to 89°51' Since the secant
function is highly unstable near a right angle, he computed a very
different value than we would: sec(87°) Earth-Moon radii i.e.
approximately 19.1 Earth-Moon radii. [The actual figure he recorded
was a range: 18 to 20 Earth-Moon radii]. We would compute the value
as between 343 Earth-Moon radii and 381 Earth-Moon radii. The
conventional value is 346 Earth-Moon radii.
A (relatively) simple way for us to replicate this measurement
uses a tool Aristarchus did not have: an accurate clock, allowing
one to measure time down to one second. [At least, that's what
occurred to us when I talked with George Fisher.] By exactly
measuring when the Moon attains first/third quarter, and
also exactly measuring when solar noon is, we can obtain an
angular displacement between the Moon at first/third quarter and
the Sun at solar noon. [4 minutes of time equals 1° of
rotation. An accuracy of 2 seconds suffices to measure down to 1
minute of accuracy.] We then apply a correction for the Sun's
movement on the ecliptic to obtain where the Sun was when the Moon
was measured at first/third quarter. Proceed from there, being
certain to use intervals for calculation.
The above is from "Mathematical Thought From Ancient to Modern
Times" by Morris Kline, Vol. 1, [section 4 "Greek Mathematical
Astronomy" of chapter 7 "The Greek Rationalization of Nature".]
The Moon
 Clementine probe
summary from the U.S. Navy
Clementine probe
summary from the U.S. Navy
Lunar Orbiter Summary
Java Current Moon Phase Calculator
- Apparent angular diameter: about 30'
Mars
Weather
from Malin Space Science Systems
Atlas
from Malin Space Science Systems
U.S. NASA's  exploration project and landing
sites
exploration project and landing
sites
This section is not completely implemented yet.
Meteors and Asteroids
Meteor shower calendar
Trojan asteroid enumeration
AA29: Almost in Earth's orbit.
This section is not completely implemented yet.
This galaxy (the Milky Way)
Extra-solar planets encyclopedia
and mirror.
Let's start with the Hertzsprung-Russell diagram, a method of
graphing stars by effective temperature (the temperature which the
star is actually radiating at, when thought of as a black-body)
against any of luminosity, apparent magnitude, or absolute
magnitude. Historically, temperature is plotted as
decreasing from left to right. The full temperature range
that can be graphed includes 2,000K° to 50,000K°. [An
example diagram will have to wait until I obtain/construct one of
sufficient quality.]
| Spectral type |
Surface temperature, in K° |
Spectroscopic features |
| O |
50,000 - 28,000
|
Ionized helium, possibly helium emission
lines
|
| B |
28,000 - 10,000
|
Neutral helium
|
| A |
10,000 - 7,400
|
Hydrogen
|
| F |
7,400 - 6,000
|
Metals, hydrogen
|
| G |
6,000 - 4,900
|
Ionized calcium, metals
|
| K |
4,900 - 3,500
|
Calcium, metals, light molecules
|
| M |
3,500 - 2,000
|
Molecules (including metal oxides), carbon
|
| Brown dwarfs |
2,000 - 1,000
|
Lithium (these don't have nuclear fusion, so the lithium
is not destroyed by being convected to the interior of the
star).
|
| Luminosity classes |
| I |
Supergiant |
| II |
Bright giant |
| III |
Giant |
| IV |
Subgiant |
| V |
Dwarf (main sequence) |
The letter classifications are due to early attempts to describe
the appearance of stars. The most important feature is that most
stars are on the "main sequence": a path generally slanting
downward with decreasing temperature. These are the stars that
primarily use hydrogen fusion as an energy source. This is
theoretically explained by a star's luminosity being strongly
correlated with its mass when it relies on hydrogen fusion as an
energy source.
It is possible to estimate the ratio of the distances of two
given star clusters from a vantage point (the only useful example
being the solar system) using the main sequence. Since stars within
a cluster are roughly at the same distance from Earth, it is
possible to chart the apparent magnitude (possibly after correcting
for absorption by interstellar gas) of the stars on the same graph.
The more distant cluster is fainter, so its main sequence will be
vertically lower on the diagram. Since the intensity of
light falls off as the square of distance, the downward shift in
apparent magnitude directly measures the factor by which the more
distant cluster is further away from Earth than the nearer
cluster.
Apparent magnitude measures how intense the (visible) light from
a star is. It is calibrated on a logarithmic scale so that a
magnitude 1 star is exactly 100 times as bright in intensity as a
magnitude 6 star.
Absolute magnitude is a statement of how intense the (visible)
light from a star would be if the star was 10 parsecs distant from
Earth (or other vantage point).
A parsec is defined as the distance that a star would have to be
at to exhibit one arc-second of parallax from opposite points on
the Earth's orbit. That is: think of the star as being at the
vertex of an isosceles triangle opposite the side which is a
diameter of the Earth's orbit. When that vertex is two seconds, the
distance from the Sun to the star is one parsec. In practice, a
decent approximation for a parsec is 3.26 light-years, where a
light-year is the distance that light travels in a year.
This suggests that there should be a formula, using a base 10
logarithm, converting luminosity to absolute magnitude. This
formula should be of the form
(absolute magnitude)=-(5/2)log10(luminosity)+b
where b is to be determined empirically for a given system of
measuring units.
If we define the Sun's current luminosity [as of 1900-2000
CE/AD] to be 1, then b is simply the estimated absolute magnitude
of the Sun : 26.74 . In contrast, the apparent magnitude of the Sun
is -4.83. This suggests that we are receiving approximately
4.24·1012 times as much energy from the Sun as if
it were at ten parsecs. Since radiation intensity falls off as the
square of the distance, this suggests that 10 parsecs is
approximately 2.06·106 times as long as 1 AU (the
average orbital distance of the Earth from the Sun).
Let's see if this checks. A parsec (by definition) is cot(1")
AU. Numerically, this is 2.062·105 AU (to four
significant digits), so 10 parsecs is 2.062·106 AU.
Apparently, the limiting factor in this exercise is how precisely
we (or the astronomers) can measure the apparent magnitude of the
Sun.
NOTE: I am using the historical sign convention for
magnitudes: increasing the magnitude number increases the
faintness of the star. Some modern references will do it the
other way around. To convert, negate the magnitude number.
A Digression: "What is Science?"
We need to get this straight now: otherwise, any discussion of the life cycle of
stars (from initial formation to old age and death) will have to be classed with
speculative thinking, comparable with Aristotle's statements about supernovae and comets.
Now, let's review how stars could form from what is actually
observed (telescopically) around us. Between stars, there are
clouds of dark, cold gas and dust that are normally visible only
when illuminated by stars. The illuminated clouds (and, by
generalization, those we don't see) are predominantly hydrogen gas
[H2]. Other molecules, of varying complexity, are also
found in these clouds. We call these molecular clouds. The largest
examples, giant molecular clouds, may have a total mass of at least
a million solar masses.
Now, "dark, cold gas and dust" suggests that the Boltzmann speed distribution for
particles (or its quantum-corrected variants) applies. Being a
large cloud, gravity is significant. If a sufficient
fraction of the cloud is caught in a vaguely central gravity field
whose escape velocity exceeds that of most of the gas particles in
the cloud...it collapses inwards. [This was first noted, in 1902,
by Sir James Jeans (1877-1946). He published analytic criteria for
the initiation of this process.]
Now, let's consider the initial stages of the collapse of a
molecular gas cloud. It is thinner than many terrestrial vacuums,
so the ideal gas laws apply (even though it is very cold). There
will be some molecular kinetic energy acquired from the cloud
falling into itself, beyond the usual ideal gas law tradeoffs
between volume (decreasing), pressure, and temperature. Also, total
angular momentum is conserved...so even if the total angular
momentum is immeasurable as a molecular gas cloud, it will
eventually cause the cloud to visibly spin.
Eventually (simulation: 100,000 years, give or take a few tens
of thousands of years?), the collapsed molecular gas cloud will
change appearance. We then call it a protostar. Protostars are
graphable on a Hertzsprung-Russell diagram -- they are large,
luminous, and cool (compared to stars).
At this point, it is critical how much mass ends up in the
would-be star (rather than its associated nebula). Less than 8% or
so of a solar mass (80 times Jupiter's mass) is fatal: hydrogen
fusion does not initiate, and the result is called a brown dwarf.
[Astronomical pluralization differs from mythological
pluralization: Seven brown dwarfs in the sky, vs. the fairy tale
"Snow White and the Seven Dwarves".]
About half of all known stars are thought to be in binary
systems. [At least, this is true within the range in which we can
resolve binary stars.] It is possible for a binary system to be one
entry in a larger "binary" system.
A stable triple star system is theoretically possible, with
very restrictive conditions...starting with all three
members being within about 1% of each other in mass, pairwise. The
corresponding orbit is a "figure eight": 8 . See
"A New Solution to the Three-Body Problem",
Notices of the American Mathematical Society (May 2001),
by Richard Montgomery
for more details. It is speculated that the incidence of these
triple star systems ranges from 1 per galaxy to 1 in the entire
universe.
Much of the above is from "The Illustrated Encyclopedia of the
Universe", ©2001 The Foundry Media Company Ltd.
This cosmos
This section is not implemented yet.
AMAZON.COM® is the registered trademark of Amazon.com, Inc.
Opinions, comments, criticism, etc.? Let me know about it.
Return to the Math page, or the main page.

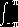
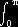 r
2sin(f)
df dq dr
r
2sin(f)
df dq dr r
2
r
2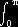 sin(f) df dr
sin(f) df dr r
2 [-cos(f)
r
2 [-cos(f) 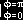 ] dr
] dr r
2 [-cos(p)+cos(0)] dr
r
2 [-cos(p)+cos(0)] dr r
2 2 dr
r
2 2 dr r
2 dr
r
2 dr
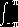
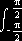 r
2cos(f)
df dq dr
r
2cos(f)
df dq dr r
2
r
2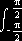 cos(f) df dr
cos(f) df dr r
2 [sin(f)
r
2 [sin(f) 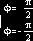 ] dr
] dr r
2 2sin(p/2)
dr
r
2 2sin(p/2)
dr r
2 2 dr
r
2 2 dr r
2 dr
r
2 dr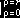 ]
]